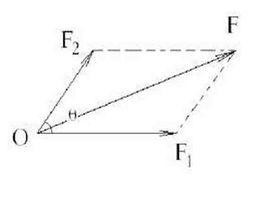
基本概念
合力矩定理:在平面匯交力系中,合力對平面內任意一點的力矩,等於其所有分力對於同一點的力矩的代數和。由公式可以表示為:
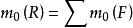 合力矩定理
合力矩定理力矩
力矩的作用是使物體繞點或軸轉動,單位是牛·米(N·m)或千牛・米(kN,m)。
力矩具有以下幾點性質:
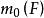 合力矩定理
合力矩定理1)在平面同題中,力F對0點之矩不僅取決於力F的大小和方向,同時還與矩心0的位置有關,矩心的位置不同,力矩的大小和轉向也不同,因此,力矩必須與矩心相對應,即指明矩心的位置,矩心的位置通常用符號 中的下標“0”來表示,不指明矩心來談力矩是沒有意義的;
2)在特殊情形下,當力的大小等於零,或力的作用線通過矩心(即d=0)時,則力矩等於零;
3)當力F沿其作用線移動時,它對任一點之矩不發生變化,因為這時力F的大小和方向以及力臂d均未改變;
4)互成平衡的兩個力對任一點之矩的代數和恆等於0,因為此二力對任一點之矩大小相等,轉向相反。
必須指出,力矩的感性概念是通過力使剛體繞固定點(或固定軸)轉動而引出的,但當抽象為具有普遍意義的概念後,作用於剛體上的力可以對剛體上任意一點取矩。即矩心不一定非要取在可以使剛體繞之轉動的固定點(或固定軸)上,而是可以取剛體上任意一點為矩心,對於非自由剛體,力對其上任意一點取矩時,剛體並不一定就繞該點轉動,但定有轉動趨勢,例如,用坂手挖緊螺後,繼保持用於坂手上的力,雖說螺帕和板手都不轉動了,但力矩卻仍然存在。
合力矩定理的證明
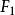 合力矩定理
合力矩定理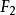 合力矩定理
合力矩定理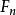 合力矩定理
合力矩定理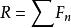 合力矩定理
合力矩定理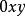 合力矩定理
合力矩定理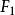 合力矩定理
合力矩定理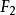 合力矩定理
合力矩定理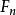 合力矩定理
合力矩定理 合力矩定理
合力矩定理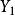 合力矩定理
合力矩定理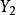 合力矩定理
合力矩定理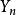 合力矩定理
合力矩定理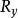 合力矩定理
合力矩定理設有平而匯交力系 , ,…, ,其合力 ,如圖1所示,在力系所在平面內任取一點0為矩心,以0點為原點,作直角坐標系 ,井使x軸通過各力的匯交點A。力 , ,…, ,和 在y軸上的投影分別為 , ,…, 和 。
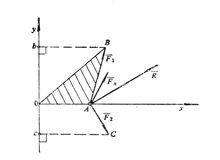 圖1
圖1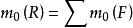 合力矩定理
合力矩定理由
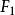 合力矩定理
合力矩定理得力 對0點之矩
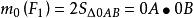 合力矩定理
合力矩定理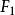 合力矩定理
合力矩定理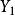 合力矩定理
合力矩定理其中線段0b是力 在y軸上的投影,因此,上式又可寫為
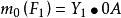 合力矩定理
合力矩定理同理可得
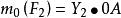 合力矩定理
合力矩定理 合力矩定理
合力矩定理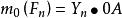 合力矩定理
合力矩定理根據合力投影定理,有
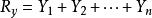 合力矩定理
合力矩定理上式兩邊同乘以0A,得
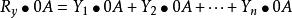 合力矩定理
合力矩定理即:
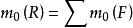 合力矩定理
合力矩定理合力矩定理雖然是從具有合力的平面匯交力系導出的,但是也適用於有合力的其它力系。