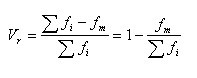計算公式1
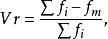 異眾比率
異眾比率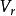 異眾比率
異眾比率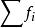 異眾比率
異眾比率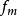 異眾比率
異眾比率其中表示異眾比率,為變數值的總頻數;為眾數組的頻數 ,m表示數組的數量。
計算公式2
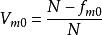 異眾比率
異眾比率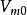 異眾比率
異眾比率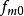 異眾比率
異眾比率其中,表示異眾比率,表示眾數次數,N表示總體單位總數(即總體次數)。
用途和意義
異眾比率主要適合測度分類數據的離散程度,當然,對於順序的數據以及數值型數據也可以計算異眾比率。它雖然也是一個反映離散程度的相對指標,但是與標準差係數不同。
異眾比率主要用於衡量眾數對一組數據的代表程度。異眾比率越大,說明非眾數組的頻數占總頻數的比重越大,眾數的代表性就越差;異眾比率越小,說明非眾數組的頻數占總頻數的比重越小,眾數的代表性越好。
異眾比率的特點
異眾比率的作用是衡量眾數對一組數據的代表程度。異眾比率越大,說明非眾數組的頻數占總頻數的比重越大,眾數的代表性就越差;異眾比率越小,說明非眾數組的頻數占總頻數的比重越小,眾數的代表性越好。
異眾比率的適用範圍
異眾比率主要用於測度分類數據的離散程度,當然,對於順序數據以及數值型數據也可以計算異眾比率。
實例
譬如,我們通過計算求出一項50人調查中,購買其它品牌飲料(指除可口可樂之外的品牌)的人數達到70%的異眾比率,異眾比率比較大,那么,說明用“可口可樂”來代表消費者購買飲料品牌的狀況,其代表性比較差,其眾數代表性就不是很明顯。