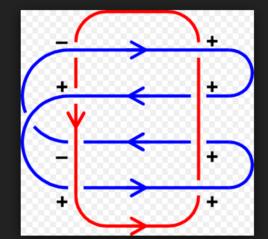
定義
空間中任何兩條閉曲線都恰好可以移動成如下標準位置之一。這決定了環繞數：
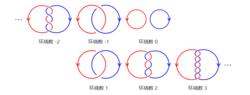環繞數每條曲線在移動過程中可以穿過自身，但這兩條曲線保持互相分離。
計算環繞數
存在一個算法計算出一個鏈環圖表的環繞數。
正交叉數總數減去負交叉數總數等於環繞數的兩倍，即
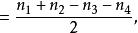環繞數環繞數
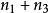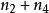環繞數
環繞數這裡 n, n, n, n分別表示四類交叉數的個數。兩個和 與總相等。這樣得到了如下另外的公式
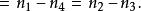環繞數環繞數
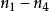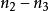環繞數
環繞數注意到只涉及到藍曲線被紅曲線下交叉，而只涉及到上交叉。
性質與例子
懷特黑德鏈環兩條曲線環繞數為零。
•任何兩條沒有連結起來的曲線相交數為零。但環繞數為零的兩條曲線仍可能是連結起來的（例如右圖的懷特黑德鏈環（Whitehead link））。
•逆轉任何一條曲線的定向，環繞數改變符號；但兩條曲線同時逆轉定向，環繞數不變。
•環繞數具有手征性：取一個鏈環的鏡像，環繞數改變符號。我們對正環繞數的約定基於右手法則。
•x-y平面上一條定向曲線的卷繞數等於它與z-軸（將z-軸想像為三維球面中一條閉曲線）的環繞數。
•更一般地，如果其中一條曲線是簡單的，則這個分支的第一同調群同構於整數Z。在此情形，環繞數由另一條曲線的同調類決定。
•在物理學中，環繞數是拓撲量子數之一例，它與量子糾纏有關。
積分定義
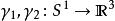環繞數
環繞數給定兩條不交可微曲線，定義從環面到單位球面 高斯映射為
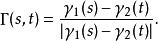環繞數
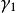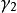環繞數
環繞數取單位球面上一點 v，從而鏈環的正交投影到垂直於 v的平面給出一個鏈環圖表。觀察到點 ( s, t) 在高斯映射下映為 v對應於鏈環圖表中一個交叉，這裡在上。並且 ( s, t) 的一個鄰域在高斯映射下映為 v的一個鄰域，保持或逆轉定向取決於交叉的符號。從而為了計算這個對應於 v的鏈環圖表的環繞數，只需數高斯映射覆蓋 v的帶符號次數。由於 v是一個正則值，這恰是高斯映射的度數（即 Γ 的像蓋住球面的帶符號次數）。環繞數的同痕不變性自動由度數在同倫下不變得到。任何其它正則值將得到相同的數，所以環繞數與任何特定的鏈環圖表無關。
曲線 γ與 γ的環繞數的這種表述給出了用二重線積分表示的一個明確公式，即 高斯環繞積分：
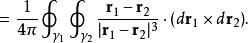環繞數環繞數
這個積分求出了高斯映射像的全部帶符號面積（被積函式是 Γ 的雅可比矩陣），然後除以球面的面積（等於 4π）。
推廣
•就像三維中環繞的閉曲線，任何兩個維數為m與n的閉流形，可能在m+n+1 維歐幾里得空間中環繞起來。任何這樣鏈環有一個相伴的高斯映射，其度數是環繞數的推廣。
•任何標架紐結（framed knot）有一個自環繞數，得自計算紐結C與將曲線C中的點沿著標架向量稍微移動得到一條新曲線的環繞數。由鉛直移動（沿著黑板標架）得到的自環繞數稱為考夫曼自環繞數（Kauffman's self-linking number）。
