背景知識
理想氣體狀態方程
理想氣體狀態方程，又稱理想氣體定律、普適氣體定律，是描述理想氣體在處於平衡態時，壓強、體積、物質的量、溫度間關係的狀態方程。它建立在玻義耳-馬略特定律、查理定律、蓋-呂薩克定律等經驗定律上。
其方程為pV = nRT。這個方程有4個變數：p是指理想氣體的壓強，V為理想氣體的體積，n表示氣體物質的量，而T則表示理想氣體的熱力學溫度；還有一個常量：R為理想氣體常數。可以看出，此方程的變數很多。因此此方程以其變數多、適用範圍廣而著稱，對常溫常壓下的空氣也近似地適用。
滿足理想氣體狀態方程且比熱比為常數的氣體，稱為完全氣體，從微觀角度來看，它是分子本身體積與分子間作用力都可以忽略不計的氣體。在常溫常壓下，實際氣體分子的體積和分子間的相互作用也可忽略不計，狀態參數基本能夠滿足理想氣體狀態方程，所以空氣動力學常把實際氣體簡化為完全氣體來處理。在低速空氣動力學中，空氣就可以被視為比熱比為常數的完全氣體；在高速空氣動力學中，氣流的溫度較高，空氣中氣體分子的轉動能和振動能隨著溫度的升高而相繼受到激發，比熱比不再是常數，在1500~2000K的溫度範圍內，空氣可視為變比熱比的完全氣體。
理想氣體分壓定律
道爾頓分壓定律（也稱道爾頓定律）描述的是理想氣體的特性。這一經驗定律是在1801年由約翰·道爾頓所觀察得到的。在任何容器內的氣體混合物中，如果各組分之間不發生化學反應，則每一種氣體都均勻地分布在整個容器內，它所產生的壓強和它單獨占有整個容器時所產生的壓強相同。也就是說，一定量的氣體在一定容積的容器中的壓強僅與溫度有關。例如，零攝氏度時，1mol 氧氣在 22.4L 體積內的壓強是 101.3kPa 。如果向容器內加入 1mol 氮氣並保持容器體積不變，則氧氣的壓強還是 101.3kPa，但容器內的總壓強增大一倍。可見， 1mol 氮氣在這種狀態下產生的壓強也是 101.3kPa 。
道爾頓（Dalton）總結了這些實驗事實，得出下列結論：某一氣體在氣體混合物中產生的分壓等於在相同溫度下它單獨占有整個容器時所產生的壓力；而氣體混合物的總壓強等於其中各氣體分壓之和，這就是氣體分壓定律（law of partial pressure）。
即理想氣體混合物中某一組分B的分壓等於該組分單獨存在於混合氣體的溫度T及總體積V的條件下所具有的壓力。而混合氣體的總壓即等於各組分單獨存在於混合氣體溫度、體積條件下產生壓力的總和。這即為道爾頓分壓定律。
道爾頓定律只適用於理想氣體混合物，實際氣體並不嚴格遵從道爾頓分壓定律，在高壓情況下尤其如此。當壓力很高時，分子所占的體積和分子之間的空隙具有可比性；同時，更短的分子間距離使得分子間作用力增強，從而會改變各組分的分壓力。這兩點在道爾頓定律中並沒有體現。
理想氣體分壓定律的推導
首先，由理想氣體狀態方程推導出理想氣體分壓定律：
PV=nRT（1）
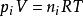理想氣體分體積定律（2）
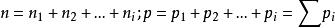理想氣體分體積定律所以，（3）
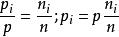理想氣體分體積定律根據（1）和（2）可以得到，；
這就是理想氣體分壓定律。
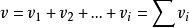理想氣體分體積定律而
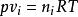理想氣體分體積定律
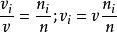理想氣體分體積定律所以，
知識擴展
實際氣體狀態方程
實際氣體都不同程度地偏離理想氣體定律。偏離大小取決於壓力、溫度與氣體的性質，特別是取決於氣體液化的難易程度。對於處在室溫及1大氣壓左右的氣體，這種偏離是很小的，最多不過百分之幾。如氧氣和氫氣是沸點很低的氣體（-183攝氏度和-253攝氏度），在25攝氏度和1大氣壓時，摩爾體積與理想值的偏差在0.1%以內。而沸點較高的二氧化硫和氯氣(-10攝氏度與-35攝氏度)，在25攝氏度與1大氣壓下就不很理想。它們的摩爾體積比按理想氣體定律預計的數值分別低了24%與16%。當溫度較低、壓力較高時，各種氣體的行為都將不同程度地偏離理想氣體的行為。此時需要考慮分子間的引力和分子本身的體積重新構造氣體狀態方程。
