簡介
球體波函式是亥姆霍茲方程的解,通過將方程寫在球狀坐標中並套用分離變數的技術,就像使用球面坐標導致球諧函式一樣。 如果使用扁球狀坐標,則稱為扁圓球形波函式,如果使用長橢球坐標,則為橢球形波函式。如果不使用亥姆霍茲方程,則採用分離變數的方法,拉普拉斯方程涉及球坐標,球形波函式減少到球面諧波。 具有扁球形坐標,解決方案稱為扁平諧波,並且具有長橢球坐標,增長諧波。 兩種類型的球形諧波可以用勒讓德函式來表示。
基本方程及推導
在球坐標中,標量波動方程為:
 球體波函式
球體波函式 球體波函式
球體波函式採用分離變數法,令,得到
 球體波函式
球體波函式 球體波函式
球體波函式 球體波函式
球體波函式連帶勒讓德函式的表達式為:
 球體波函式
球體波函式 球體波函式
球體波函式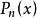 球體波函式
球體波函式 球體波函式
球體波函式 球體波函式
球體波函式式中,為勒讓德函式。與相應的另一獨立解為,方程一般解可寫為:
 球體波函式
球體波函式 球體波函式
球體波函式令,則v(r)滿足:
 球體波函式
球體波函式這是一個半奇數的貝塞爾方程,其解為:
 球體波函式
球體波函式定義球貝塞爾函式為;
 球體波函式
球體波函式 球體波函式
球體波函式 球體波函式
球體波函式 球體波函式
球體波函式 球體波函式
球體波函式對於球內的散射場,可取基本波函式為:
 球體波函式
球體波函式對於球外的散射場,可取基本波函式為:
 球體波函式
球體波函式同樣,可以由基本波函式的疊加來表示任意波場:
 球體波函式
球體波函式對貝塞爾函式的物理意義與貝塞爾函式的物理意義相似零階球貝塞爾函式有簡單的表達式為:
 球體波函式
球體波函式 球體波函式
球體波函式 球體波函式
球體波函式 球體波函式
球體波函式高階球貝塞爾函式也有顯明的初等函式表達式。
