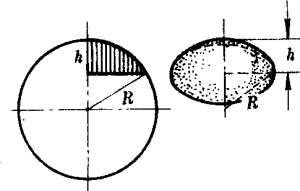
定義
用一個平面去截一個球的一部分,不大於一個半球,所得的餘下的部分叫球缺。
計算
球缺的面積=2πRH(不包括截面的面積)
球缺體積公式=(π/3)(3R-H)*H^2(R是球的半徑,H是球缺的高) 球缺
球缺球缺質心:勻質球缺的質心位於它的中軸線上,並且與底面的距離為:c = (4R-H)H/(12R-4H) = (d^2+2H^2)H/(3d^2+4H^2)
(其中,H為球缺的高,R為大圓半徑,d為球缺的底面直徑。)
用高等數學定積分來計算的方法:
已知:球半徑R,球缺高H。我們就可以得到球缺的體積為:
V=πH^2(R-H/3)
證明過程:
由於圓方程(原點為零點):
∵X 2 + Y 2 = R 2
∴X=( R 2 - Y 2 )½
∴V球缺=∫ πx^2 dy=π∫ (R^2-y^2) dy (積分上限為R 積分下限位R-H)
推導後得出
V=πH^2(R-H/3)
又:球缺高H,底面半徑r,則V=[πH(3r^2+H^2)]/6
區別
球缺與球冠球缺屬於幾何體,是指用一個平面去截一個球所得的部分,是“體”的概念。而球冠只是個“面”的概念,是指一個球面被一個平面所截得的部分。
因此,球缺可以計算體積;而球冠只能計算面積。