簡介
等徑圓球的堆積有最密堆積和其他形式的堆積，最密堆積的結構可以從密堆積層來了解。密堆積層的結構只有一種形式，如下圖：
密堆積層的結構A表示球心位置，B表示頂點向上三角形空隙中心位置，C表示頂點向下三角形空隙中心位置。在層中每個球和周圍6個球接觸，即配位數為6，在密堆積層中，每個球周圍有6個三角形空隙，每個空隙由三個球組成。這些三角形空隙分為兩類，它們的頂點朝向相反。
由密堆積層進行堆積時。若採用最密堆積的方式，必須是堆積層中的每個球正好對準相鄰一層中的一類三角形空隙，即每一個球都同時和相鄰一層的3個球相接觸。按照這種方式將密堆積層堆積起來，才能形成最密堆積的空間結構。按照這個原則作最密堆積寸，各密堆積層的相對位置實質上只有三種情況，這可把各層球心所處的相對位置投影到上圖中標明的A、B、C三種位置上來加以區分。
堆積方式
常見的最密堆積結構有兩種，即立方最密堆積和六方最密堆積。下面主要討論立方最密堆積和六方最密堆積方式，簡要介紹圓球的立方體心密堆積和簡單立方堆積。
1、立方最密堆積
將密堆積的相對位置按照ABCABC ABC…方式作最密堆積，這時重複的周期為3層，如圖（a）所示，由於從這種最密堆積方式中可劃出面心立方品胞，故稱為立方最密堆積，記為A型堆積。
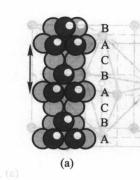立方最密堆積示意圖2、六方最密堆積
將密堆積的相對位置按照ABABAB…方式作最密堆積，其重複周期為兩層，如圖（b）所示。由於這種堆積方式可劃出六方晶胞，故稱為六方最密堆積，記為A型堆積。除上述兩種最密堆積外，最密堆積方式還有ABAC…和ABABCBCAC等形式。
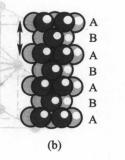六方最密堆積示意圖3、立方體心密堆積
立方體心密堆積，記為A2型堆積。但這種密堆積並不是最密堆積，堆積係數為0.6802。立方體心密堆積結構中，每個圓球均有8個最近的配位球，處在立方體的8個頂點上；另外還有6個稍遠一點的配位球，所以有效配位數可看作8和14之間。
4、簡單立方堆積 ·
簡單立方堆積是密堆積程度更差的一種圓球堆積方式，它是8個圓球堆成一個立方體，這種堆積方式的堆積係數是0.5236，配位數是6，只形成立方體空隙。
堆積特點
（1）各種形式的最密堆積中，每個球的配位數均為12，即每個球有12個最相近鄰的球，這12個球中，有6個球與中心球處於同一密堆積層，另外6個球分別位於與中心球相鄰的上下密堆積中。
（2）有相同的堆積密度，其堆積係數即空間利用率均為0.7405。堆積係數即球體積與整個堆積體積之比，可按下圖中的立方最密堆積的一個晶胞進行計算。
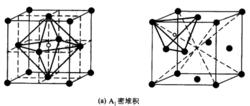A1型密堆積
球密堆積設球的半徑為R，晶胞邊長為a，面對角線長為4R，它等於 a，所以
球密堆積 球密堆積 球密堆積a=4R/ =2 R，晶胞體積V=a3=16 R 。
晶胞內4個圓球的總體積V=4×（4πR /3）=16πR /3。
堆積係數=V/V=0.7405。
（3）在各種最密堆積中，球間的空隙類型、數目和大小也相同。由N個半徑為尺的球組成的最密堆積中，平均有2N個四面體空隙，可容納半徑為0.225R的小球；還有N個八面體空隙，可容納半徑為0.414R的小球。
舉例
金屬單質的結構
若將金屬鍵看作原子間各向同性的相互作用，金屬原子在晶體中總是趨向於最緊密的方式堆積，即按立方最密堆積A1或六方最密堆積A3進行排列。
例如屬於A型的金屬晶體有Al、Sr、Ni、Pd、Pt、Cu、Ag、Au、Pb等；屬於A型的Be、Mg、Sc、Ti、Co、Zn、Cd等；屬於A型的有Li、Na、K、Rb、Cs、V、Nb、Ta、Cr、Mo、W等。由於溫度和壓力等外界條件的改變，有些金屬可以有不同的構型，如α-Fe為A型，γ-Fe為A型。
離子晶體的堆積方式
許多離子晶體的結構可以按密堆積結構了解其特徵，一般負離子半徑較大，可把負離子看作等徑圓球進行密堆積，而正離子有序地填人負離子所形成的某種空隙之中。根據離子晶體的組成，空隙的占有分數不同，有的能將某種空隙全部填滿，有的只是部分填人。
下面列舉幾種離子晶體的堆積方式：
1、在NaCI結構中，Cl-離子以A型密堆積，Na 離子占據全部八面體空隙。若以密堆積層的形式描述，Cl 離子堆積層的相對位置用A、B、C表示，小的正離子Na 在層中的相對位置用a、b、c表示，沿堆積層的法線方向NaCI中正、負離子的堆積周期∣AcBaCb∣。
2、ZnS的結構可看作S 的最密堆積，Zn 填充在一半四面體空隙之中，填隙時互相間隔開。使填隙四面體不會出現共面連線或共邊連線。在立方ZnS結構中，S 採取立方最密堆積，按密堆積層的形式描述，其結構可表達為∣AaBbCc∣。在六方ZnS結構中，S 採取六方最密堆積，密堆積層堆積表示式∣AaBb∣
3、CaF的晶體結構可看作F-的簡單立方堆積，Ca 填人立方體空隙中，由於Ca 數目比F 少一倍，所以有一半空隙是空的，只有一半的立方體空隙填Ca ，Ca 與空位交替地在空間間隔排列。CaF晶體也可看作Ca 的立方最密堆積，F 填在全部的四面體空隙中。
