模型建立
Lotka-Volterra(1925,1926)假設在沒有捕食者時，獵物種群呈指數增長：
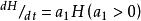獵物-捕食者模型捕食者種群在沒有獵物時呈指數下降：
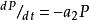獵物-捕食者模型若兩個種群置入有限空間時，獵物種群的增長率降低。降低的多少依賴於捕食者的密度：
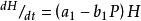獵物-捕食者模型同樣，捕食者種群的增長依賴於獵物種群的密度：
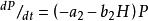獵物-捕食者模型
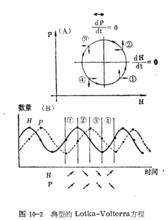10-2
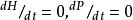獵物-捕食者模型平衡點 時
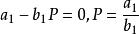獵物-捕食者模型
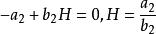獵物-捕食者模型 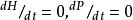獵物-捕食者模型系統的定性解為中心解，為周期性解。當種群初始值不時，以不同的封閉曲線圍繞奇點(奇點即的點)星逆時針旋轉(見圖10-2)
模型改進
該方程顯然有許多不足之處。例如：1）如無P，H呈指數增長。 2）H種群僅因P而死亡。3）P僅以H為食。4）兩種群均無密度制約作用。故在原方程的基礎上可做大量工作；改進一項或兩項使之更符合生物學意義， 再進行定性分析。例如Volterra(1926) 構想無捕食者時(或寄生物，意義相同)，獵物種群服從邏輯斯蒂方程，其它不變。方程形式為:
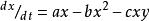獵物-捕食者模型
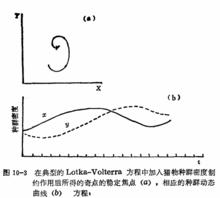10-3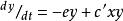
獵物-捕食者模型
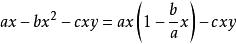獵物-捕食者模型其中，第一式：
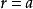獵物-捕食者模型
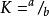獵物-捕食者模型顯然，邏輯斯蒂方程中的內稟自然增長率 ， 環境載力 ，其奇點為穩定焦點。如圖10-3(a)。Leslie和Gower (1948) 考慮到應加進去兩個種群間的密度制約關係。方程如下：
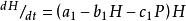獵物-捕食者模型
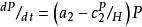獵物-捕食者模型
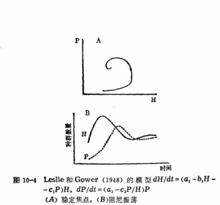10-4此方程中的第一式同於Volterra(1926)方程中的第一式，加入了獵物種群的自飽和項。
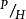獵物-捕食者模型 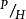獵物-捕食者模型 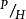獵物-捕食者模型第二式中以 代替H，以體現當獵物少而捕食者多時， 值增大，不利於捕食者種群的增長。反之，若獵物多而捕食者少時， 值小，有利於捕食者種群的增長。
其奇點也為穩定焦點，如圖10-4A。繪成種群曲線時(圖10-4B)，兩種群隨時間而阻尼振盪，最後均達到平衡密度並共存下去。
