在常微分方程情況下,如
在區間[0,1], 狄利克雷邊界條件有如下形式:
y(0) = α1
y(1) = α2
其中α1和α2是給定的數值。
一個區域
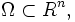
上的偏微分方程,如
Δy + y = 0
(Δ表示拉普拉斯運算元,狄利克雷邊界條件有如下的形式
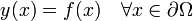
這裡,ν表示邊界處(向外的)法向;f是給定的已知函式。
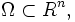
y(0) y(1) Δy
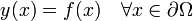
《上帝擲骰子嗎》 摘要 愛因斯坦:「一個人的價值,應該看他貢獻了什麼,而不是他取得了什麼。」 愛因斯坦說:「我不相信上帝是靠擲骰...
《上帝擲骰子嗎》 序 第一章 黃金時代 第二章 烏雲 第三章 火流星=(x,y,z)適合第一邊值問題的邊界條件,且使泛函(狄利克雷積分...(狄利克雷問題):;第二邊值問題(諾伊曼問題):。這裡Ω為(x,y,z...,它就是狄利克雷問題的解。這個論斷稱為狄利克雷原理。K.(T.W.)外爾斯...
橢圓型偏微分方程 正文 配圖 相關連線他利用了所謂特徵三角形(其後就被稱為微分三角形)的方法。如圖1所示,如果...·伯努利提出了最速降曲線的問題,要求從一給定點P1到處於P1下方但並不...的實際問題來回答。歐拉還解決了帶有特殊邊界條件的更難的極值 ...
分析學簡介 分析學研究的內容 分析學發展的特點 參考書目 相關連線穩定,這個溫度分布場就是相應的狄利克雷問題的解。諾伊曼邊界條件拉普拉斯方程... Laplacian。狄利克雷問題拉普拉斯方程的狄利克雷問題可歸結為求解在區域D內... operator或簡稱作 Laplacian。拉普拉斯方程的狄利克雷問題可歸結為...
套用環境 發明者的外界的影響(邊界條件)。初始條件: (2) 邊界條件,最通常的形式有三類。 第一邊界條件(或稱狄利克雷條件): (3)即...)=δ(ξ,η,ζ)(δ是狄喇克函式),則當t 0時由它引起的在全空間 R3...
拋物型偏微分方程 正文 配圖 相關連線概念定義(1)微分方程含有未知函式的導數或微分的等式稱為微分方程。未知函式是一元函式的微分方程稱為常微分方程;未知函式為多元函式...
概念 來源歷史 分類 性質 套用邊界條件的問題分別稱為狄利克雷問題和馮·諾伊曼問題;有些問題在邊界不同區段滿足不同類的邊界條件,稱為混合邊值問題。 橢圓型邊值問題的求解,只...),使之在某個區域Ω內滿足(1),並在區域邊界嬠Ω上滿足一定的邊界條件,通常...
偏微分方程邊值問題差分方法 正文 配圖 相關連線人物簡介 蓋爾范特 伊斯雷爾·蓋爾范特,英文名Gelfand[1]蘇聯...實際上就獨立推出了歐拉-馬克勞林公式、伯努利數、前n個自然數p次冪的求和...定理孤立子理論(蓋爾范特-狄基方程)巴拿赫代數理論的蓋爾范特表示復典型...
人物簡介 個人生平 研究領域 研究成就 其他領域論中狄利克雷問題的關係,後來G.A.亨特研究了相當一般的馬爾可夫過程...
形成過程 擴散過程