概述
狀態評估是當代電力系統能量管理系統(EMS)的重要組成部分,尤其在電力市場環境中發揮更重要的作用。狀態評估問題的提出激發了許多學者的研究興趣,他們以數學、控制理論和其它新理論為指導,根據當時的計算機軟體和硬體條件,結合電力系統的特點,在理論方面進行廠大量研究。同時,以狀態評估軟體實用為目標,針對實際工程面臨的問題,探索和總結出許多可行的寶貴經驗。狀態評估的理論研究促進了工程套用,而狀態評估軟體的工程套用也推動了狀態評估理論的研究和發展。迄今為止,這兩方面都取得了大量成果。然而,狀態評估領域仍有不少問題未得到妥善解決,隨著電力系統規模的不斷擴大,電力工業管理體制向市場化邁進,對狀態評估有了新要求,各種新技術和新理論不斷湧現,為解決狀態評估的某些問題提供了可能。
狀態評估方法
在確定性情形下,線性系統的狀態評估的主要方法有呂恩伯格觀測器。只有系統的能觀測部分(見能觀測性)的狀態才能重構,而且能以任意快的速度來重構,但在具體實現時則受到噪聲、靈敏度等因素的限制。在系統的裝置或其觀測通道受有隨機噪聲干擾時,則必須用統計估計方法來處理。依觀測數據與被估狀態在時間上的相對關係,狀態評估又可區分為平滑、濾波和預報3種情形。為了估計t時刻的狀態x(t),如果可用的信息包括t以前的觀測值,就是平滑問題。如果可用的信息是時刻t的觀測值,估計可實時地進行,稱為濾波問題。如果必須用時刻(t-Δ)以前的觀測來估計經歷了Δ時間之後的狀態x(t),則是預報問題。狀態評估中所套用的方法屬於統計學中的估計理論。最常用的是最小二乘估計,其他如風險準則的貝葉斯估計、最大似然估計、隨機逼近等方法也都有套用。不管是維納濾波還是卡爾曼濾波,這些方法都只適用於線性系統,而且需要對被估計過程有充分的知識。對於非線性系統或對動態系統特性不完全了解的複雜估計問題,還需要深入研究。工程上可用一些近似計算方法來處理,常見的有基於局部線性化思想的廣義卡爾曼濾波器、貝葉斯或極大後驗估值器和可以根據濾波過程的歷史知識自動修改參數的自適應濾波或預報技術等。
狀態評估器的估計準則
狀態評估的數學模型是基於反映網路結構、線路參數、狀態變數和實時量測之間相互關係的量測方程:
z=h(x)+v
其中z是量測量;二是狀態變數,一般是節點電壓幅值和相位角;二是量測誤差;二和二都是隨機變數。
狀態評估器的估計準則是指求解狀態變數二的原則,電力系統狀態評估器採用的估計準則大多是極大似然估計,即求解的狀態變數二`使量測值z被觀測到的可能性最大,用數學語言描述,即:
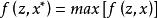 狀態評估
狀態評估其中f(z)是量測z機率分布密度函式。
顯然,具體的目標函式表達式與量測z的分布模式密切相關,對每個f(幼都有相應的極大似然估計函式。對同一系統的相同實時量測,若假定的量測分布模式不同,則得到的估計結果不完全相同,因此有不同估計準則的估計器。
舉例
電力系統狀態評估是電力系統調度中心的能量管理系統(EMS)的核心功能之一,其功能是根據電力系統的各種量測信息,估計出電力系統當前的運行狀態。現代電網的安全經濟運行依賴於能量管理系統(EMS),而能量管理系統的眾多功能又可分成針對電網實時變化進行分析的線上套用和針對典型潮流斷面進行分析的離線套用兩大部分。電力系統狀態評估可以說是大部分線上套用的高級軟體的基礎。如果電力系統狀態評估結果不準確,後續的任何分析計算將不可能得到準確的結果。

