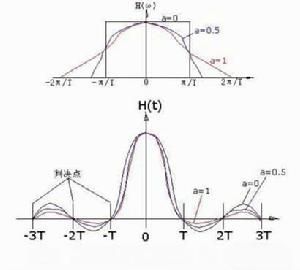
無失真函式
無失真傳輸是主要傳輸特性通常可以用其幅頻曲線和相頻曲線來描述。無失真傳輸要求振幅特性與頻率無關,即其振幅頻率特性曲線是一條直線;要求其相位特性是一條通過原點的直線,或者等效地要求其傳輸群時延與頻率無關。
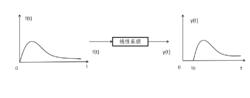 數位訊號的無失真傳輸
數位訊號的無失真傳輸 無失真傳輸
無失真傳輸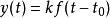 無失真傳輸
無失真傳輸如果激勵信號為f(t),無失真傳輸的回響為y(t), 為延遲時間,k為與t無關的常實數,稱為波形比例係數衰減的比例係數,應滿足: (式1) .
無失真傳輸條件
若要保持系統的無失真傳輸信號,從頻域分析,可對式1兩邊取傅立葉變換,並利用其時移性,有
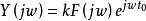 無失真傳輸
無失真傳輸由於
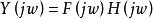 無失真傳輸
無失真傳輸所以無失真傳輸的系統函式為(式2)
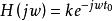 無失真傳輸
無失真傳輸即
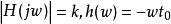 無失真傳輸
無失真傳輸因此,無失真傳輸系統在頻域應滿足兩個條件:
(1)系統的幅頻特性在整個頻域範圍內應為常數k,即系統的通頻帶為無窮大;
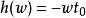 無失真傳輸
無失真傳輸(2)系統的相頻特性在整個頻率範圍內應與w成正比,即 ,如圖2所示。
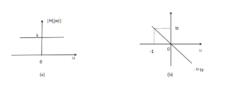 無失真傳輸對系統函式的要求
無失真傳輸對系統函式的要求若對式2取傅立葉反變換,則可知系統的單位衝激回響為
 無失真傳輸
無失真傳輸h(t)=kδ(t-)(式3).
該式表明,一個無失真傳輸系統,其單位衝擊回響仍為一個衝激函式,不過在強度上不一定為單位1,位置上也不一定位於t=0處。因此,式3從時域給出了無失真傳輸系統的條件。
無失真傳輸系統的幅頻特性應在無限寬的頻率範圍內保持常量,這是不可能實現的。實際上,由於所有的信號其能量總是隨頻率的增高而減少,因此,系統只要有足夠大的頻寬,以保證包含絕大多數能量的頻率分量能夠通過,就可以獲得較滿意的傳輸質量。
信號失真
線性系統引起的信號失真的原因
各頻率分量幅度產生不同的衰減——幅度失真
各頻率分量產生的相移不與頻率成正比,回響的各頻率分量在時間軸上的相對位置產生變化——相位失真
信號失真的分類
通常將失真分為以下兩大類。
1、線性系統的失真:幅度,相位變化,不產生新的頻率成。
2、非線性系統的失真:產生新的頻率成分。