簡介
漂移電晶體也稱為緩變基區電晶體,就是它的基區摻雜濃度的分布是緩慢變化的,則其基區中存在有能加速少數載流子運動的自建電場,故有漂移電晶體之稱。由於基區自建電場對少數載流子的加速作用,漂移電晶體的放大性能和頻率性能等都比均勻基區電晶體的要優越。現在所使用的Si平面電晶體等,基區都是通過擴散摻雜來形成的,因此也都是漂移電晶體(只有合金電晶體可認為是均勻基區電晶體)。
對漂移電晶體,其基區的電子電流既有擴散電流, 也有漂移電流,在基區摻雜濃度是指數分布的情況下(表面濃度小,裡面濃度大),在基區中可得到恆定的漂移電場。漂移電晶體的所有性能都可以在均勻基區電晶體的基礎上簡單地給出:只要採用Gummel數來代替均勻基區電晶體的有關表示式中的基區寬度和是基區摻雜濃度即可;Gummel數就是單位面積中性基區的雜質總量。
內建電場的形成
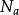 漂移電晶體
漂移電晶體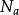 漂移電晶體
漂移電晶體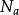 漂移電晶體
漂移電晶體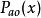 漂移電晶體
漂移電晶體 漂移電晶體
漂移電晶體若npn電晶體基區的有效受主濃度是x的函式,則多子(空穴)因存在濃度梯度將會擴散,使原來小處帶正電荷,大處帶負電荷。正、負電荷所產生的電場,稱為內建電場。此電場反過來又造成空穴的漂移運動,其方向與擴散運動方向相反。如用代表平衡空穴濃度,代表內建電場,則:
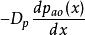 漂移電晶體
漂移電晶體空穴的擴散流密度=
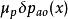 漂移電晶體
漂移電晶體空穴的漂移流密度=
平衡時,空穴的兩種電流之和應為0,即:
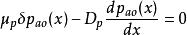 漂移電晶體
漂移電晶體在利用愛因斯坦關係,可得內建電場:
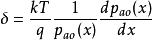 漂移電晶體
漂移電晶體漂移電晶體中的少子分布和少子電流
在推導緩變基區少子分布及少子電流時有兩種方法:
(1)求解包括漂移分量在內的少子連續性方程,得出少子分布和少子電流分布,從而導出緩變基區電晶體,I-U方程,這種方法稱為精確法,其過程繁雜;
(2)近似法,即忽略少子在基區輸運過程中的複合損失,認為基區少子電流近似為常數。這是分析緩變基區電晶體時除指數分布近似外的另一個廣泛採用的近似,下面就採用這一近似方法分析。
在基區由於有自建電場,注入電子在基區不僅有擴散運動,也有在自建電場作用下的漂移運動,因此電子電流為:
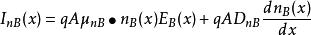 漂移電晶體
漂移電晶體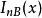 漂移電晶體
漂移電晶體忽略基區符合損失時,為常數,一般用通過發射結的電子電流代替,於是有:
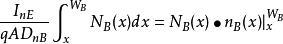 漂移電晶體
漂移電晶體當電晶體偏置在有源放大區時,集電結邊緣處電子密度為零,將邊界條件代入得:
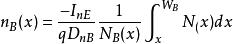 漂移電晶體
漂移電晶體經過指數分布近似及化簡得:
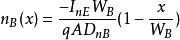 漂移電晶體
漂移電晶體上式正是均勻基區電晶體工作於有源放大區時的基區少子分布函式。
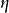 漂移電晶體
漂移電晶體下圖畫出了不同電場因子下基區電子濃度分布曲線,圖中採用了歸一化坐標。
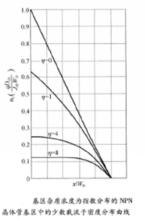 NPN電晶體基區中的少數載流子密度分布曲線
NPN電晶體基區中的少數載流子密度分布曲線合金擴散電晶體
這種電晶體的發射結是合金結,集電結是擴散結,其管芯結構和雜質分布如下圖所示。由圖可見,發射結為突變結,集電結為緩變結,基區雜質分布有一定的梯度,故稱梯度基區電晶體或緩變基區電晶體。合金擴散電晶體具有較好的高頻特性,可用於高速開關、高頻放大等場合。合金擴散電晶體一般是用鍺製造的 。
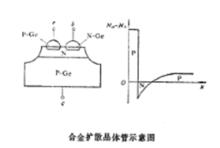 合金擴散電晶體示意圖
合金擴散電晶體示意圖
