簡介
流體作湍流運動時所產生的應力,除了粘性應力外尚有附加的應力,包括法向附加應力和切向附加應力,這些附加的應力都是湍流所特有的,是由於流體質點的脈動產生的 , 稱為湍流應力。
因而湍流應力可以分為切應力和正應力,而流動切應力又可以分為雷諾切應力和黏性切應力兩部分。
物理意義
對於不可壓縮粘性流動,在不考慮質量力的情況下, N-S 方程具有下列形式:
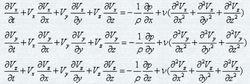 湍流應力
湍流應力式(1)
著名的不可壓縮流體作湍流運動時的時均運動方程,即雷諾方程:
 湍流應力
湍流應力式(2)
將時均運動方程和 N-S 方程相比可以看出,湍流中的應力,除了由於粘性所產生的應力外,還有由於湍流脈動運動所形成的附加應力,這些附加應力稱為湍流應力。雷諾方程與 N-S 方程在形式上是相同的,只不過在粘性應力項中多出了附加的湍流應力項。
將雷諾方程與粘性流體應力形式的動量方程進行比較,由式(2)可以看出,在湍流的時均運動中,除了原有的粘性應力分量外,還多出了由脈動速度乘積的時均值
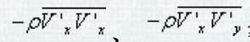 湍流應力
湍流應力等構成的附加項,這些附加項構成了一個對稱的二階張量,即
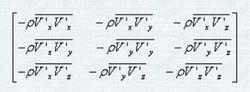 湍流應力
湍流應力式(3)
式(3)中的各項構成了所謂的湍流應力。
湍流應力的測量和計算方法
PIV是一種利用散布在流體內的示蹤粒子在光平面的反射光來測量瞬時速度場的可視化測量技術。
湍流應力測量試驗中用一個相機在不同時刻記錄示蹤粒子的圖像,這樣示蹤粒子的位移就可以通過對示蹤粒子圖像的處理而測量出來。通常PIV測量使用一個雷射器作為光源,測量時這個光平面的位置需要精確定位,這樣就可以實現在光平面內的流動測量。
結果顯示,測量的雷諾剪下應力最大值是關於流動測量坐標方向的函式。這個特性使得實驗結果分析複雜化,尤其是當流動方向與測量坐標系不同或者在測量區域內不同時。進一步來說,測量系統坐標系的方向不一定是雷諾應力最大值所對應的坐標系的方向,這點對於將雷諾應力與衡量血液破壞程度相關聯時顯得尤為重要。
一個有效的處理方式就是求出流動區域內的正應力和切應力的最大值,這就是常提到的“主雷諾正應力”和“主雷諾剪下應力”,它定義為正應力(或切應力)張量沿正應力(或切應力)主軸方向(即正應力或切應力的最大值方向)的應力。雖然全張量是三維的,但在PIV二維測量平面內的正應力(或切應力)主軸以及相應的主正應力(或主切應力)可以通過如下理解進行計算:它等於或者小於三維主正應力(或切應力)的真實值。
恆星演化過程中湍流應力作用
在恆星演化過程中,對流起著極其重要的作用,一方面對流的混合作用對化學組成的分布、核燃燒的產生有重要的影響,另一方面對流的傳能、傳壓以及對流與振動的耦合作用,又對恆星內部的溫度分布、壓強、密度等產生重要的影響。特別是當恆星演化到巨星分支和漸近巨星分支階段時,恆星的整個外殼處於對流狀態,並且對流區內通過對流作用的傳能遠大於輻射作用的傳能。所以在研究恆星的結構與演化時,對流作用是不能被忽略的。在恆星內部對流作用表現為複雜湍流運動,有學者將對流作用考慮為湍流壓的形式引入到恆星的外層演化,計算了湍流壓對恆星結構與演化的影響。實際上氣體的湍流運動存在著巨觀上的“表現應力”。
研究結果表明:對於中等質量恆星,湍流作用對恆星結構與演化的影響主要是由於在恆星外部對流區內湍流所表現出來的巨觀應力相對於引力而言較大,改變了流體的靜力學平衡,從而影響恆星的結構與演化。
