特性原理
 流體微團運動
流體微團運動由於流場速度分布不均勻,流體微團各點的速度不相等而產生平移、轉動、線變形和角變形等4種運動形式。流體微團不同於剛體之處是除了平移和轉動外還有變形 。
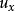 流體微團運動
流體微團運動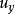 流體微團運動
流體微團運動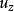 流體微團運動
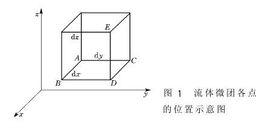
流體微團運動對於直角坐標系,在流場中任取正交微小六面體的流體微團如圖1所示。設A點速度為 、 、 ,則其他各點的速度用泰勒級數展開,忽略高階微量後如表所示。
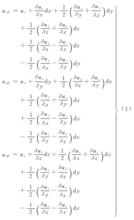 流體微團運動
流體微團運動對E點的速度進行改寫,可以得出(1)式:
流體微團運動速度分解
由於流體微團上各點的速度不同,經過dt時段後,該流體微團不僅位置發生了移動,而且形狀也將發生變化,由原來的正交微小六面體變成斜平行微小六面體。由速度分解可以看出,流體微團的運動形式包括以下兒種 。
平移
 流體微團運動
流體微團運動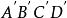 流體微團運動
流體微團運動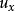 流體微團運動
流體微團運動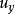 流體微團運動
流體微團運動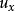 流體微團運動
流體微團運動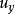 流體微團運動
流體微團運動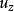 流體微團運動
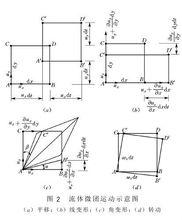
流體微團運動微團運動過程中任一線段的長短及方位均保持不變的運動。這隻有在各點的速度都相同的情況下才能實現。以圖1中的ABCD面為例,如果平移到 ,則必須是各點速度均為、,見圖2(a)。在式(1)中右邊第1項 、 、 ,正是圖1所示六面體微團上各點所共同具有的速度,稱為平移速度。
線變形
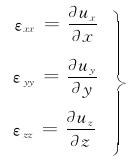 流體微團運動
流體微團運動微團運動過程中軸線的伸長或縮短。它是由於軸線上各點沿軸線方向的速度不同所產生的。如果ABCD發生線變形後變成,見圖2(b),則x方向單位時間內單位長度的線變形是如右所示
式中,為線變形率。式(1)右邊第2項即代表與線變形相應的速度增量。
角變形
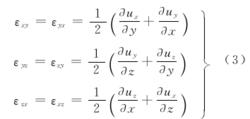 流體微團運動
流體微團運動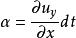 流體微團運動
流體微團運動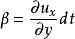 流體微團運動
流體微團運動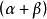 流體微團運動
流體微團運動微團運動過程中兩條垂直邊夾角的變化。它是由於軸線上各點沿垂直軸線方向的速度不等所產生的。圖1中的A和B因y方向速度不同使AB轉動,轉角近似為公式;A和C因x方向速度不同,使AC轉到,轉角近似為,見圖2(c)。轉角可以分成角變形和轉動兩部分。規定單位時間內轉角的一半為角變形率,即
式(1)右邊第三、四項代表與角變形相應的速度增量。
轉動
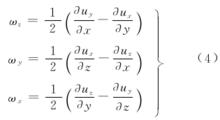 流體微團運動
流體微團運動微團運動過程中互相垂直的軸線方位的變化。它也是由於軸線上各點沿垂直軸線方向的速度不等所產生的。中扣除角變形之外就是微團單純的轉動角。單位時間的轉動角度為角轉速,其值為式(4)
式(1)右邊第5、6項代表與轉動相應的速度增量。見圖2(d)。
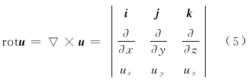 流體微團運動
流體微團運動角轉速的兩倍定義為速度旋度,又稱渦量,寫成式(5)
流體的運動根據微團是否繞自身順時軸轉動分成有渦流動與無渦(有勢)流動(參見勢流、渦流) 。