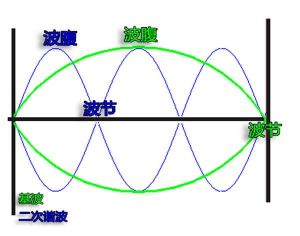
概述
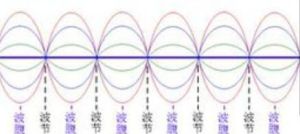 波腹
波腹波函式中的振幅最大的點、線或曲面。駐波中振幅最大的位置。波函式是量子力學中描寫微觀系統狀態的函式。在經典力學中,用質點的位置和動量(或速度)來描寫巨觀質點的狀態,這是質點狀態的經典描述方式,它突出了質點的粒子性。
由於微觀粒子具有波粒二象性,粒子的位置和動量不能同時有確定值(見測不準關係),因而質點狀態的經典描述方式不適用於對微觀粒子狀態的描述,物質波於巨觀尺度下表現為對幾率波函式的期望值,不確定性失效可忽略不計。
詮釋
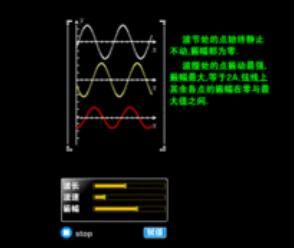 波函式
波函式波函式是機率波。其模的平方代表粒子在該處出現的機率密度。既然是機率波,那么它當然具有歸一性。即在全空間的積分。然而大多數情況下由薛丁格方程求出的波函式並不歸一,要在前面乘上一個係數N,即把它帶入歸一化條件,解出N。至此,得到的才是歸一化之後的波函式。注意N並不唯一。波函式不是買彩票的中獎幾率,彩票的中獎幾率是線性相加的,買兩張彩票,中獎幾率就變為2倍,買N張彩票,中獎幾率就是N倍。
波函式具有相干性,具體地說,兩個波函式疊加,機率並非變成12+12=24倍,而是在有的地方變成(1+1)2=4倍,有的地方變成(1-1)2=0,具體取決於兩個波函式的相位差。聯想一下光學中的楊氏雙縫實驗,不難理解這個問題。
相關定義
駐波:兩列振幅相同的相干波在同一直線上沿相反方向傳播時互相疊加而成的波,稱為駐波。
橫波:橫波的特點是質點的振動方向與波的傳播方向相互垂直。在橫波中波長通常是指相鄰兩個波峰或波谷之間的距離。電磁波就是橫波。
波腹:在駐波場中幅值為最大的點、線或面。
波節:在駐波場中幅值最小(一般為0)的點、線或面。