汪萊(1768～1813)
正文
中國清代數學家。字孝嬰,號衡齋,安徽歙縣人。生於乾隆三十三年,卒於嘉慶十八年。出身於貧苦家庭,幼年受教育不多,但他愛學習,“不由師傅,深造自得”,自學了數學、天文、測量、樂律和經史等知識。1807年到北京考取八旗官教習，在國史館纂修天文志、時憲志（即民用曆書）。汪萊的工作以數學最為突出，遺作經學生夏燮整理，出版《衡齋算學》七冊。這是他在1796～1805年寫成的數學研究成果，其中第五、六兩冊還吸取了友人李銳、焦循的意見。
汪萊在數學上的貢獻主要有以下幾方面：
①方程論 在深入研究秦九韶、李冶正負開方術的基礎上，他對24個二次方程（他稱為一乘方形）、72個三次方程(二乘方形)逐個討論，認為高次方程的正根應有幾個，只取其中一個根作為完整答數是不恰當的。由此他歸結出當一般二次方程、三次方程不止有一個正根時,方程的係數應具備的條件,他並總結了三次方程的根與係數的一般關係。其結果相當於說,如方程αx3-bx2+сx-d=0有三個正根α，β，у，那么有
(
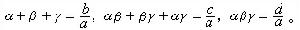
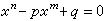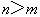都是自然數,
,
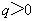)有正根的條件是：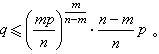 
②球面三角形的解 汪萊在《衡齋算學》的第一冊中系統地討論了球面三角形六種基本問題的求解，分別得出了有解和無解的條件。例如第四種問題：已知兩邊及一對角且這一個對角小於一象限時，汪萊對全部19種有解、無解情況中的11種都有正確論斷。
③組合公式 《衡齋算學》對組合公式有專題研究，所獲公式相當於如下結果：
