原理
次最佳方塊編碼
統計分析表明,比特平面中有兩種結構的方塊經常出現:m×n個全“0”和全“1”,並且前者出現的機率多於後者,於是可得出如下的次最佳方塊編碼方案
全“0”子塊:碼字為“0”
全“1”子塊:碼字為“11”
其他情況:碼字為“10”+“xxx…x”
“xxx…x”為將子塊的比特內容直接輸出,故又稱為直接編碼。
這種編碼方案的平均碼長L為:
L=P(0;n,m)+2P(1;n,m)+(2+nm)[1-P(0;n,m)-P(1;n,m)]=nm[1-P(0;n,m)-P(1;n,m)]+2- P(0;n,m) (41.77)
式中:P(0;n,m)和P(1;n,m)分別為m×n個全“0”或全“1”子塊出現的機率。
壓縮比C=nm/L,將L代入可得:
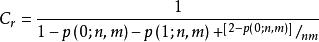 比特面編碼
比特面編碼(41.78)
可見,C是P(0;n,m)和P(1;n,m)的遞增函式。
用格雷碼錶示像素亮度
通常,數位化後像素的電平值都是PCM自然二進制碼,這種碼的特點是高位最重要的比特平面圖形簡單,並適用於上述方塊編碼,但重要性稍差的比特面圖形相當複雜,尤其低位最不重要的比特平面噪聲為主要成份,因而不適宜用方塊編碼。這樣,由高位4個最重要的比特面獲得的壓縮效益將被其他幾個低位比特面所抵消,其原因在於對於PCM編碼,若相鄰像素的亮度值變化一個等級,其碼字也可能相差好幾個比特。改進的方法是用格雷碼來表示像素的亮度。由於格雷碼的特點是碼距惟一,使得比特面上取值相同的面積增大,即P(0;n,m)和P(1;n,m)增大,因而增大了壓縮比。
視覺心理編碼
視覺心理編碼是指,允許恢復圖像有一定的失真,只要視覺感覺不出或可以容忍。具體做法是把子塊內不超過K個“1”的子塊視為全“0”子塊,而把不超過K個“0”的子塊視為全“1”子塊,這樣也等效於取值相同的面積增大,即P(0;n,m)和P(1;n,m)增大,因而也提高了壓縮比。
據實驗表明,若子塊大小為n=m=4,當K=6時引起的失真人眼尚可接受。
方塊尺寸的選擇
在壓縮比Cr的表示式中,它與n,m的關係是複雜的。當nm增加時,1/nm減少,但很可能導致P(0;n,m)和P(1;n,m)減少。因而nm不能盲目增大。實驗表明,取n=m=4較為合適。
