定義
靜態圖像編碼是研究怎樣利用圖像固有的統計特性(信源特性),以及視覺的生理學、心理學特性(信宿特性),或者記錄設備(如普通照相底片)和顯示設備(如電視、監示器)等的特性,經過壓縮編碼從原始圖像信息中提取出有效信息,儘量去掉那些無用的冗餘信息,以便高效率地進行圖像的數字傳輸或數字存儲;而在復原時仍能獲得與原始圖像相差不多的復原圖像,即保持圖像信息中的有效信息。
分類
靜態圖像的編碼方法主要分為PCM法和壓縮編碼法兩大類,其中壓縮編碼法又分為預測法、變換法、平均信息法、內插法、運動補償法和其他方法等六小類。每個小類下都有相關的具體算法。
背景
方塊截斷編碼也稱為方塊編碼,是一種用於灰度圖像的有損數據壓縮算法。這種算法將圖像分為以方塊為單位,在每一方塊中,在保持原有平均數和標準方差(即保持二階矩)的同時,減少灰度等級,以達到壓縮的目的。方塊截斷編碼是普渡大學的O.R.Mitchell和E.J.Delp兩位教授於1979年首先提出的。
編碼方法
設圖像中的一個子塊的大小為m=N×N個像素,子塊中第i個像素為Pi,其亮度值為Xi,方塊的兩個代表性亮度為a0、a1,稱之為亮度級分量,用一個二元碼φi指明像素Pi編碼後屬於a0或a1,φi稱為分辨力分量。設方塊內的亮度閾值為XT,像素Pi編碼後的電平值為Yi,則基本編碼方法可用下式表示:
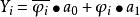 方塊編碼
方塊編碼(1.1)
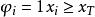 方塊編碼
方塊編碼(1.2)
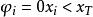 方塊編碼
方塊編碼由(1.1)和(1.2)式可知,編碼後方塊的像素亮度{Y1,Y2,…,Ym}可以用{a0,a1}和{φ1,φ2,…,φm}的組合表示,用它們作為傳輸內容,收端也能恢復出編碼圖像。其中前面兩個元素一般具有與亮度值相同的等級,而後者為一個m比特的比特面,因此可以降低傳輸數碼率。
設a0、a1各用Pbit,則編碼後每個像素的平均比特數為:
B=(m+2p)/m=1+2p/m (1.3)
由於a0、a1是用來代表亮度層次的,一般需要6~8bit,如取m=4×4,P=8,則經方塊編碼後可壓縮到每像素2bit。
由(1.3)式可見,m越大,B越小,即壓縮比越高。但此時圖像質量也下降,因為方塊尺寸越大,子塊內像素的相關性也越小,只用兩個灰度作近似,逼真度當然就越差。通常m=4×4是比較折衷的方式。
參數的選擇
m一定時,編碼參數a0、a1及X的選擇對恢復圖像的質量有很大的影響。下面是兩種較為典型的方案。
(1)保持一階矩、二階矩的參數選擇
 方塊編碼
方塊編碼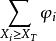 方塊編碼
方塊編碼取閾值X ,並記:q= ,它為編碼後亮度為a1的像素的個數。編碼策略是保持子塊的一階矩和二階矩不變,即:式(1.4)
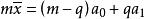 方塊編碼
方塊編碼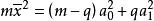 方塊編碼
方塊編碼解此方程組可得式(1.5):
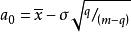 方塊編碼
方塊編碼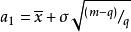 方塊編碼
方塊編碼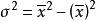 方塊編碼
方塊編碼其中 為子塊的均方差。
(2)均方誤差最小的參數選擇
 方塊編碼
方塊編碼取X ,編碼策略是使均方誤差最小,即:
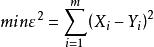 方塊編碼
方塊編碼(1.6)
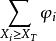 方塊編碼
方塊編碼同樣,記q= ,可以得出:
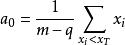 方塊編碼
方塊編碼(1.7)
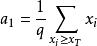 方塊編碼
方塊編碼由於a0、a1分別是小於和大於閾值X的像素的平均值,因此有時記作X和X。
 方塊編碼
方塊編碼以上介紹的是兩種比較簡單的方案。由於算法中已指定了X ,所以實現起來比較方便。在一些場合還可以再增加一個方程,作為XT或q的限制條件,這樣可以增加一些保持信息,但同時也增加了算法的複雜性。
需要指出的是,方塊編碼是非信息保持型編碼,它相當於只使用了兩個電平的量化器,而且在套用中因為取整也會引入一些附加的誤差。
降低數碼率的方法
在方塊尺寸固定的情況下,可以從兩方面著手進一步降低碼率。
①選擇合適的傳輸用的量度級分量,通過成組編碼的方式降低傳輸碼率。
對於上面的方案(1),根據(1.5)式,可以用和取代a0、a1進行傳輸,收端則同樣可以恢復編碼圖像。
研究發現,人的視覺有這樣的特性,當圖像的方差大時,即亮度變化大時,對圖像的平均值不太敏感;而當圖像方差小,即亮度變化平緩時,要求所傳輸的平均值要儘量精確些。根據這一特性,對編碼參數作這樣的組合,方差大時,傳輸平均值所用的比特少,即對平均值進行了粗量化,反之,則用較多的比特數。表1.1是實現這種組合的一個例子。原圖像亮度有32個層次,若分別對和傳輸,共需5+4=9bit,而根據表中的組合,共有128種,僅需7bit,因此碼率得以降低,而引入的誤差對人眼的觀察是不敏感的。
表1.1 方差與平均值成組編碼及所需碼字數
| s |  方塊編碼 方塊編碼 | 所需的碼數 |
| 0 | 0-31 | 32 |
| 1 | 1-22,24,26,28,30 | 26 |
| 2 | 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31 | 16 |
| 3 | 2,5,8,11,14,17,20,23,26,29 | 10 |
| 4 | 2,5,8,11,14,17,20,23,26,29 | 10 |
| 5 | 2,6,10,14,18,22,26,30 | 8 |
| 7 | 2,6,10,14,18,22,26,30 | 8 |
| 9 | 3,8,13,18,23,28 | 6 |
| 11 | 4,10,16,22,28 | 5 |
| 13 | 6,12,19,26 | 4 |
| 15 | 10,16,22 | 3 |
| 總計 | 128 |
 方塊編碼
方塊編碼 方塊編碼
方塊編碼對於方案(2),採用{X, }或{ ,X}作為傳輸亮度級,則根據下式同樣可以恢復編碼圖像。
 方塊編碼
方塊編碼m =(m-q)X+qX(1.8)
 方塊編碼
方塊編碼 方塊編碼
方塊編碼 方塊編碼
方塊編碼 方塊編碼
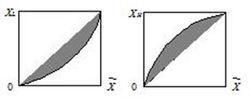
方塊編碼實驗表明,{X, }和{ ,X}的統計分布大部分集中在45°斜線附近,如圖1.1所示。這表明,對於{X, }和{ ,X},很多組合是很少出現甚至不出現,編碼時可以省去許多碼字。而分別對各亮度級分量進行編碼,相當於把所有的組合都考慮在內。因此,成組編碼比分別編碼減少了碼字總數,即降低了碼率。
 方塊編碼
方塊編碼圖1.1兩種不同參數組合的分布
採用成組編碼降低碼率的理論依據,通常稱之為矢量量化編碼。
②通過比特面的再劃分,降低傳輸數碼率。
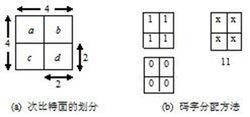
例如,子塊尺寸為4×4時,可將比特面分為4個2×2的次比特面,如圖1.2(a)所示。實驗發現,次比特面a,b,c,d為全0或全1的相對次數要高,而其他情況很少出現,於是採用圖1.2(b)的碼字分配方法就可以實現比特面碼率的降低。
 方塊編碼
方塊編碼圖1.2比特面的劃分與編碼
參考文獻
圖像編碼基礎(第3版)姚慶棟畢厚傑王兆華徐孟俠等編著清華
