正邏輯與負邏輯的概念
用電平的高和低表示邏輯值1和0的關係並不是唯一的。既可以規定用高電平表示邏輯1、低電平表示邏輯0，也可以規定用高電平表示邏輯0，低電平表示邏輯1。這就引出了正邏輯和負邏輯的概念。
通常，把用高電平表示邏輯1，低電平表示邏輯0的規定稱為 正邏輯。反之，把用高電平表示邏輯0，低電平表示邏輯1的規定稱為 負邏輯。
事實上，同一邏輯函式的正邏輯和負邏輯所表示的函式式是一對對偶式。
例1 試分別用正邏輯和負邏輯寫出圖1所示電路的邏輯表達式。
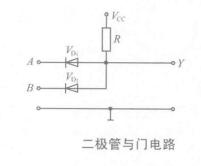圖1解：按正邏輯分析，其邏輯真值表如表1所示，邏輯表達式為Y=AB。按負邏輯分析，其邏輯真值表如表2所示，邏輯表達式為Y=A+B。
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| A | B | Y |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
由負邏輯真值表寫出的表達式為Y=A+B和由正邏輯真值表寫出的表達式Y=是對偶式。
正邏輯門與負邏輯門的關係
對於同一電路，正邏輯與負邏輯的規定不涉及邏輯電路本身的結構與性能好壞，但不同的規定可使同一電路具有不同的邏輯功能。
例2 對於某一邏輯電路，從正邏輯和負邏輯的兩個角度去分析它的邏輯關係，會得到截然不同的結果。例如圖2所示電路，設VD、VD、VD均為理想二極體，輸入高電平H=5V，低電平L=0V，則輸出端P與輸入端A、B、C的邏輯關係見表2。
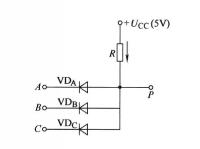圖2二極體電路| A | B | C | P |
| L | L | L | L |
| L | L | H | L |
| L | H | L | L |
| L | H | H | L |
| H | L | L | L |
| H | L | H | L |
| H | H | L | L |
| H | H | H | H |
| A | B | C | P |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| A | B | C | P |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 |
從正邏輯的角度看，該電路的真值表見表3。顯然表3的真值表說明圖1所示電路是一個二極體“與”門電路；若從負邏輯電路來看，即用高電平H表示邏輯“0”，低電平L表示邏輯“1”，則可得到真值表，見表4，從表4不難看出圖1所示電路是一個二極體“或”門電路。
由此可以得出這樣的結論：正邏輯“與”門和負邏輯“或”門在功能上所給出的結果是一樣的。也就是說，正“與”門和負“或”門是同一邏輯電路的兩種不同名稱。
由於正負邏輯之間存在著簡單的對偶關係，要將正邏輯和負邏輯相互轉換並不困難，辦法是將邏輯式中的“0”和“1”對換，這樣一來，則有：
1) 正邏輯“與”門等同於負邏輯“或”門。
2) 正邏輯“或”門等同於負邏輯“與”門。
3) 正邏輯“與非”門等同於負邏輯“或非”門。
4) 正邏輯“或非”門等同於負邏輯“與非”門。
5) 正邏輯“異或”門等同於負邏輯“同或”門。
6) 正邏輯“同或”門等同於負邏輯“異或”門。
例3 假定某邏輯門電路的輸入為A、B，輸出為F。電路輸入/輸出電平關係如表5所示。若按正邏輯規定，則可得到表6所示的真值表，由真值表可知，該電路是一個正邏輯的與門；若按照負邏輯規定，則可得到表7所示的真值表，由真值表可知，該電路是一個負邏輯的或門。由此可見，正邏輯與門等於負邏輯或門。
| A | B | F |
| L | L | L |
| L | H | L |
| H | L | L |
| H | H | H |
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
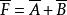正邏輯
正邏輯上述邏輯關係可以用反演規則證明。假定一個正邏輯與門的輸出為F，輸人為A、B，即有F=A B。根據反演規則，可得 。這就是說，若將一個邏輯門的輸出和所有輸入都反相，則正邏輯變為負邏輯。據此，可將正邏輯門轉換為負邏輯門。幾種常用邏輯門的正、負邏輯符號變換如圖3、4所示。
正邏輯表示的正與、正或、正與非、正或非（如圖3）分別等效於負邏輯表示的負或、負與、負或非、負與非（如圖4）。
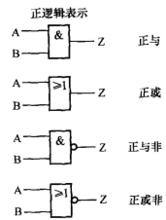圖3
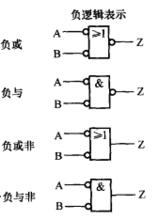圖4