正方向[數學用語]

正方向是人們規定的一個方向，與正方向相反的是負方向。在數軸中，它是三要素之一；在坐標系中，它也是不可或缺的一部分。引入“正方向”的概念的目的是更好地分析和表示問題。

數軸中的正方向

在數學中，人們用畫圖的方式把數軸“直觀化”。通過用一條直線上的點表示數，這條直線叫做數軸。

它滿足三個條件：

（1）在直線上任取一個點表示數0，這個點叫做原點；

（2）通常規定直線上從原點向右（或向上）為正方向，從原點向左（或下）是負方向；

正方向[數學用語]

正方向[數學用語]

（3）選取適當的長度為單位長度，直線上從原點向右，每隔一個單位長度取一個點，依次表示 ；從原點向左，用類似的方法依次表示

正方向的力量

“數軸，通常規定向右為正方向，因此，在數軸上右邊的數總比左邊的數大。”

“在數軸上明確方向很重要，當規定向右為正方向時，在數軸上越往右，表示的數越大；越往左表示的數就越小。”

“兩個數在數軸上的左右位置即決定了兩個數的大小。故此，數軸上的方向很重要，方向即決定了數的大小。”

“明確了方向後，還要確定原點。當規定原點即0的位置後，才能確定了正數與負數的分界點。”

“原點0右邊的點表示正數；原點0左邊的點表示負數。”

“從原點起往右，離開原點的距離的長短，決定了這個正數的數值的大小。同是兩個正數，離開原點的距離較長的正數較大，離開原點距離較短的正數較小。”

“從原點起往左則恰好相反，離開原點的距離越遠，表示的數越小。同是兩個負數，離開原點的距離較短的數較大；離開原點的距原較長的數教小。”

“由此可見，方向很重要，明確方向後，及時找準起點同樣重要。只有明確了方向，找準的起點才能更加準確的知道這個數到底有多大。”

空間直角坐標系中的正方向

為了確定空間中任意一點的位置，需要在空間中引進坐標系，最常用的坐標系是空間直角坐標系。

如圖，OBCD-D′A′B′C′是單位正方體，以A為原點，分別以OD，OA′，OB的方向為正方向，建立三條數軸x軸，y軸，z軸，這時建立了一個空間直角坐標系O-xyz， 如下圖

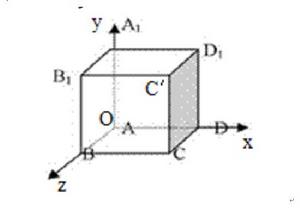圖1 建立空間直角坐標系

1）O叫做坐標原點；

2）x 軸，y軸，z軸叫做坐標軸；

3）過每兩個坐標軸的平面叫做坐標平面；

4）x軸和y軸的方向即為定義的正方向
右手表示法：令右手大拇指、食指和中指相互垂直時，可能形成的位置。大拇指指向為x軸正方向，食指指向為y軸正向，中指指向則為z軸正向，這樣也可以決定三軸間的相位置。

任意點坐標表示：空間一點M的坐標可以用有序實數組（x，y，z）來表示，有序實數組（x，y，z）叫做點M在此空間直角坐標系中的坐標，記作M（x，y，z）（x叫做點M的橫坐標，y叫做點M的縱坐標，z叫做點M的豎坐標）。