定義
函式的正實性
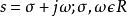 正實性
正實性 正實性
正實性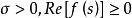 正實性
正實性 正實性
正實性設 s為一個複數, s可寫成 。如果實函式 對於 ,則稱 為 正實函式。
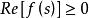 正實性
正實性 正實性
正實性如果存在λ>0,當 σ≥-λ 時, ,則稱 為 嚴格正實函式。
矩陣的正實性
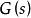 正實性
正實性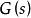 正實性
正實性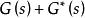 正實性
正實性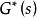 正實性
正實性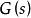 正實性
正實性一個實函式矩陣為 正實矩陣的條件是:對於滿足 Re s> 0 的複數 s,為半正定的Hermite矩陣。其中 是 的共軛轉置矩陣。如果對於Re s≥ 0,都有以上結論,則為 嚴格正實矩陣。
性質
正實函式在開的右半複平面內解析,沒有極點。
正實矩陣的所有元素在開的右半複平面內解析,沒有極點。
對於嚴格正實,以上性質變為在閉的右半複平面。
1.正實函式在開的右半複平面內解析,沒有極點。
2.正實矩陣的所有元素在開的右半複平面內解析,沒有極點。
3.對於嚴格正實,以上性質變為在閉的右半複平面。
相關定理
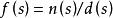 正實性
正實性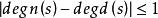 正實性
正實性1. 如果有理函式是正實的,那么。
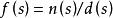 正實性
正實性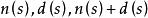 正實性
正實性2. 如果有理函式是嚴格正實的,那么都是Hurwitz多項式。
套用
在波波夫超穩定性理論中,控制系統在滿足輸入輸出乘積積分值的限定情況下,系統的超穩定性等價於系統傳遞函式矩陣的正實性,系統的超漸近穩定性等價於系統傳遞函式矩陣的嚴格正實性。因此常通過求解系統傳遞函式矩陣的正實性來判斷系統的超穩定性。
