定義
機器學習中的一個核心問題是設計不僅在訓練數據上表現好,並且能在新輸入上泛化好的算法。在機器學習中,許多策略顯式地被設計為減少測試誤差(可能會以增大訓練誤差為代價)。這些策略被統稱為正則化。
正則化是通過對學習算法的修改以減少泛化誤差而不是訓練誤差的策略。有些策略向機器學習模型添加限制參數的額外約束。有些策略向目標函式增加參數值軟約束的額外項。如果仔細選擇,這些額外的約束和懲罰可以改善模型在測試集上的表現。有時侯,這些約束和懲罰被設計為編碼特定類型的先驗知識;其他時候,這些約束和懲罰被設計為偏好簡單模型,以便提高泛化能力。有時,懲罰和約束對於確定欠定的問題是必要的。其他形式的正則化(如集成方法)結合多個假說來解釋訓練數據。
目標
在深度學習的背景下,大多數正則化策略都會對估計進行正則化。 估計的正則化以偏差的增加換取方差的減少。一個有效的正則化是有利的 ‘‘交易’’,也就是能顯著減少方差而不過度增加偏差。
在模型族訓練的過程中,存在 3 個情形:
(1)不包括真實的數據生成過程——對應欠擬合和含有偏差的情況;
(2)匹配真實數據生成過程;
(3)除了包括真實的數據生成過程,還包括許多其他可能的生成過程——方差(而不是偏差)主導的過擬合。
正則化的目標是使模型從第三種情況轉化為第二種情況。
在實踐中,過於複雜的模型族不一定包括目標函式或真實數據生成過程,甚至也不包括近似過程。我們幾乎從未知曉真實數據的生成過程,所以我們永遠不知道被估計的模型族是否包括生成過程。然而, 深度學習算法的大多數套用都是針對這樣的情況,其中真實數據的生成過程幾乎肯定在模型族之外。 深度學習算法通常套用於極為複雜的領域,如圖像、音頻序列和文本,本質上這些領域的真實生成過程涉及模擬整個宇宙。從某種程度上說,我們總是持方枘(數據生成過程)而欲內圓鑿(我們的模型族)。
這意味著控制模型的複雜度不是找到合適規模的模型(帶有正確的參數個數)這樣一個簡單的事情。相反,我們可能會發現,或者說在實際的深度學習場景中我們幾乎總是會發現,最好的擬合模型(從最小化泛化誤差的意義上)是一個適當正則化的大型模型。
參數範數懲罰
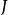 正則化運算元
正則化運算元 正則化運算元
正則化運算元正則化在深度學習的出現前就已經被使用了數十年。 線性模型,如線性回歸和邏輯回歸可以使用簡單、直接、有效的正則化策略。許多正則化方法通過對目標函式 添加一個參數範數懲罰 ,限制模型(如神經網路、 線性回歸或邏輯回歸)的學習能力。我們將正則化後的目標函式記為
 正則化運算元
正則化運算元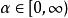 正則化運算元
正則化運算元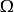 正則化運算元
正則化運算元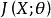 正則化運算元
正則化運算元 正則化運算元
正則化運算元 正則化運算元
正則化運算元其中, 是權衡範數懲罰項 和標準目標函式 相對貢獻的超參數。將 設為 0 表示沒有正則化。 越大,對應正則化懲罰越大。
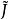 正則化運算元
正則化運算元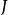 正則化運算元
正則化運算元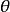 正則化運算元
正則化運算元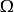 正則化運算元
正則化運算元當訓練算法最小化正則化後的目標函式 時,它會降低原始目標 關於訓練數據的誤差並同時減小參數 的規模(或在某些衡量下參數子集的規模)。選擇不同的參數範數 會偏好不同的解法。
L2 參數正則化
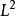 正則化運算元
正則化運算元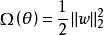 正則化運算元
正則化運算元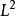 正則化運算元
正則化運算元權重衰減(weight decay)的 參數正則化通過向目標函式添加一個正則項 使權重更加接近原點。在其它領域, 也被稱為嶺回歸或Tikhonov正則。
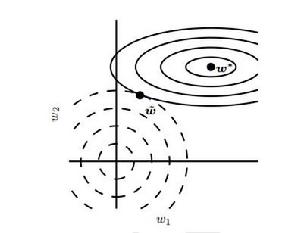 圖1 L2正則化對最佳 w 值的影響
圖1 L2正則化對最佳 w 值的影響 正則化運算元
正則化運算元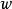 正則化運算元
正則化運算元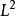 正則化運算元
正則化運算元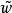 正則化運算元
正則化運算元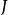 正則化運算元
正則化運算元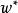 正則化運算元
正則化運算元 正則化運算元
正則化運算元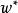 正則化運算元
正則化運算元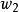 正則化運算元
正則化運算元圖1為 (或權重衰減)正則化對最佳 值的影響。實線橢圓表示沒有正則化目標的等值線。虛線圓圈表示 正則化項的等值線。在 點,這兩個競爭目標達到平衡。目標函式 的 Hessian 的第一維特徵值很小。當從 水平移動時, 目標函式不會增加得太多。因為目標函式對這個方向沒有強烈的偏好,所以正則化項對該軸具有強烈的影響。正則化項將 拉向零。而目標函式對沿著第二維遠離 的移動非常敏感。對應的特徵值較大,表示高曲率。因此, 權重衰減對 的位置 影響相對較小。
L1 參數正則化
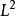 正則化運算元
正則化運算元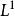 正則化運算元
正則化運算元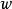 正則化運算元
正則化運算元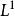 正則化運算元
正則化運算元權重衰減是權重衰減最常見的形式,除此之外,還可以使用其它方法限制模型參數的規模。比如, 正則化。形式地,對模型參數 的 正則化被定義為:
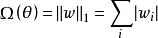 正則化運算元
正則化運算元即各個參數絕對值之和。
作為約束的範數懲罰
 正則化運算元
正則化運算元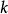 正則化運算元
正則化運算元通過構造一個廣義Lagrange函式來最小化帶約束的函式,即在原始目標函式上添加一系列懲罰項,每個懲罰項是一個係數之間的乘積,被稱為Karush-Kuhn-Tucker乘子,以及一個表示約束是否滿足的函式。如果我們想約束 小於某個常數 ,可以構建廣義Lagrange函式
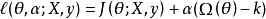 正則化運算元
正則化運算元這個約束問題的解由下式給出
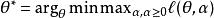 正則化運算元
正則化運算元矩陣求逆的正則化
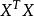 正則化運算元
正則化運算元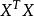 正則化運算元
正則化運算元 正則化運算元
正則化運算元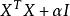 正則化運算元
正則化運算元在某些情況下,為了正確定義機器學習問題, 正則化是必要的。 機器學習中許多線性模型,包括線性回歸和 PCA,都依賴於求逆矩陣 。只要 是奇異的,這些方法就會失效。當數據生成分布在一些方向上確實沒有差異時,或因為例子較少(即相對輸入特徵( 的列)來說)而在一些方向上沒有觀察到方差時,這個矩陣就是奇異的。在這種情況下, 正則化的許多形式對應求逆 。這個正則化矩陣可以保證是可逆的。
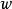 正則化運算元
正則化運算元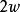 正則化運算元
正則化運算元 正則化運算元
正則化運算元相關矩陣可逆時,這些線性問題有閉式解。沒有閉式解的問題也可能是欠定的。一個例子是套用於線性可分問題的邏輯回歸。如果權重向量 能夠實現完美分類,那么 也會以較高似然實現完美分類。類似隨機梯度下降的疊代最佳化算法將持續增加 的大小,理論上永遠不會停止。在實踐中,數值實現的梯度下降最終會達到導致數值溢出的超大權重,此時的行為將取決於程式設計師如何處理這些不是真正數字的值。
大多數形式的正則化能夠保證套用於欠定問題的疊代方法收斂。例如,當似然的斜率等於權重衰減的係數時, 權重衰減將阻止梯度下降繼續增加權重的大小。
