概念
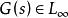 特普利茨運算元
特普利茨運算元 特普利茨運算元
特普利茨運算元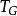 特普利茨運算元
特普利茨運算元令 ,則一個 的特普利茨運算元可用 表示,定義為
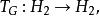 特普利茨運算元
特普利茨運算元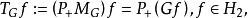 特普利茨運算元
特普利茨運算元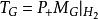 特普利茨運算元
特普利茨運算元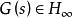 特普利茨運算元
特普利茨運算元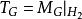 特普利茨運算元
特普利茨運算元即 。特別地,若 ,則 。
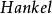 特普利茨運算元
特普利茨運算元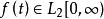 特普利茨運算元
特普利茨運算元類比於 運算元,特普利茨運算元也存在一個相應的時域描述:對 ,有
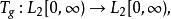 特普利茨運算元
特普利茨運算元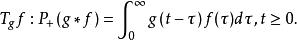 特普利茨運算元
特普利茨運算元可見,在頻域中的乘積運算元或在時域中的卷積運算元在Hankel和特普利茨(Toeplitz)運算元的發展中扮演了一個重要的角色。事實上,乘積運算元可分解成若干Hankel和特普利茨(Toeplitz)運算元。
基本原理
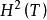 特普利茨運算元
特普利茨運算元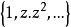 特普利茨運算元
特普利茨運算元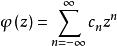 特普利茨運算元
特普利茨運算元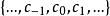 特普利茨運算元
特普利茨運算元 特普利茨運算元
特普利茨運算元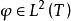 特普利茨運算元
特普利茨運算元取定 的自然正交基 ,令 。如果雙向序列 定義的特普利茨矩陣誘導了特普利茨運算元 ,那么必然 。此時
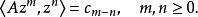 特普利茨運算元
特普利茨運算元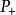 特普利茨運算元
特普利茨運算元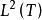 特普利茨運算元
特普利茨運算元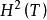 特普利茨運算元
特普利茨運算元設 是 到 上的正交投影,易見
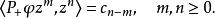 特普利茨運算元
特普利茨運算元定義具有符號的特普利茨運算元
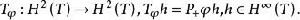 特普利茨運算元
特普利茨運算元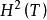 特普利茨運算元
特普利茨運算元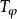 特普利茨運算元
特普利茨運算元這是 上的一個稠定運算元。因此研究由特普利茨矩陣誘導的特普利茨運算元等同於研究特普利茨運算元 。
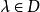 特普利茨運算元
特普利茨運算元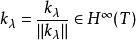 特普利茨運算元
特普利茨運算元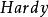 特普利茨運算元
特普利茨運算元對 ,設 是正則化的 再生核。如果上面定義的特普利茨運算元是有界的,則有
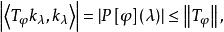 特普利茨運算元
特普利茨運算元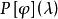 特普利茨運算元
特普利茨運算元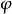 特普利茨運算元
特普利茨運算元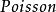 特普利茨運算元
特普利茨運算元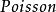 特普利茨運算元
特普利茨運算元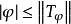 特普利茨運算元
特普利茨運算元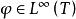 特普利茨運算元
特普利茨運算元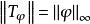 特普利茨運算元
特普利茨運算元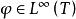 特普利茨運算元
特普利茨運算元這裡 是 的 積分。利用 積分的性質,在圓周上成立 。從這個不等式,易見 ,且 。因此研究特普利茨矩陣的問題歸結為由符號 定義的特普利茨運算元的理論。

