定義
 正交變換
正交變換 正交變換
正交變換線上性代數中, 正交變換是線性變換的一種。對一個由空間投射到同一空間的線性轉換,如果轉換後的向量長度與轉換前的長度相同,則為正交變換。
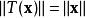 正交變換
正交變換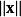 正交變換
正交變換 正交變換
正交變換其中在空間內,n表示維度。
 正交變換
正交變換 正交變換
正交變換 正交變換
正交變換 正交變換
正交變換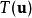 正交變換
正交變換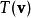 正交變換
正交變換對於正交變換T以及兩個向量和,和之內積等於正交轉換後之向量和之內積。
 正交變換
正交變換 正交變換
正交變換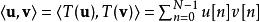 正交變換
正交變換其中N為向量長度,u[n]和v[n]分別為和之元素,正交變換不會影響轉換前後向量間的夾角和內積長度。
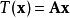 正交變換
正交變換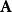 正交變換
正交變換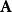 正交變換
正交變換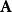 正交變換
正交變換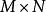 正交變換
正交變換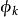 正交變換
正交變換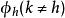 正交變換
正交變換在矩陣表示形式上,如果為正交變換,則為正交矩陣,對於正交變換之正交矩陣,其每個列互為正交,令為之矩陣,取兩個不相同的列和遵守下列關係。
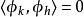 正交變換
正交變換等價刻畫
設σ是n維歐式空間V的一個線性變換,於是下面4個命題等價
1.σ是正交變換;
2.σ保持向量長度不變,即對於任意α∈V,丨σ(α)丨=丨α丨;
3.如果ε_1,ε_2,...,ε_n是標準正交基,那么σ(ε_1),σ(ε_2),...,σ(ε_n)也是標準正交基;
4.σ在任意一組標準正交基下的矩陣是正交矩陣。
正交矩陣
定義:n級實矩陣A稱為正交矩陣,如果A*A=E。(A*表示A的共軛轉置,E是單位矩陣)
分類
設A是n維歐式空間V的一個正交變換σ在一組標準正交基下的矩陣
若丨A丨=1,則稱σ為第一類正交變換,
若丨A丨=-1,則稱σ為第二類正交變換。
性質
 正交變換
正交變換 正交變換
正交變換 正交變換
正交變換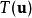 正交變換
正交變換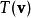 正交變換
正交變換(1)正交變換不會改變向量間的正交性,如果和正交,則和亦為正交。
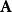 正交變換
正交變換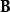 正交變換
正交變換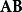 正交變換
正交變換(2)如果和皆為正交矩陣,則亦為正交矩陣。
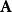 正交變換
正交變換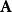 正交變換
正交變換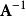 正交變換
正交變換(3)如果為正交矩陣,的反矩陣亦為正交矩陣。
(4)正交變換容易做反運算。
 正交變換
正交變換 正交變換
正交變換 正交變換
正交變換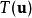 正交變換
正交變換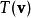 正交變換
正交變換 正交變換
正交變換 正交變換
正交變換(5)對於正交變換,如果和可以做內積,和做內積之值等於和做內積之值。
套用
正交變換的種類非常的廣,像是discrete Fourier transform、discrete cosine, sine, Hartley transforms、Walsh Transform, Haar Transform等都屬於正交變換。對矩陣做旋轉或是鏡射也屬於正交變換。

