定義
平面的一個點變換，如果保持點之間的距離不變。則稱它為正交變換(或保距變換) 。
平面正交變換的性質
從定義可知正交變換具有下述性質：
性質1 正交變換的乘積仍是正交變換。
性質2 恆等變換是正交變換。
性質3 (1) 正交變換把共線的三點變成共線的三點，且保持它們的順序不變。
(2) 正交變換把不共線的三點變成不共線的三點 。
證： (1)設A，B，C是共線的三點，且B位於A，C之間，正交變換σ把A，B，C分別變成A'，B'，C'，則|A'B'|=|AB|，|A'C'|=|AC|，|B'C'|=|BC|，由假設，|AB|+|BC|=|AC|，則|A'B’|+|B'C'|=|A'C'|，這表明A'，B'，C'三點共線，且B'在A'C'之間。
(2)設D，E，F是不共線的三點，則|DE|+|EF|>|DF|，設正交變換σ把D，E，F分別變成D'，E'，F'，則|D’E’|十|E'F'|>|D'F'|，這表明D'，E'，F'三點不共線。
由性質3即得
性質4 正交變換把直線變成直線，把線段變成線段。
性質5 正交變換是可逆的，且逆變換仍是正交變換。
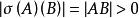平面正交變換
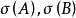平面正交變換
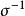平面正交變換 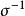平面正交變換證： 設σ是正交變換，A，B是平面上不同的兩個點，則，即σ把不同的點A，B變成不同的點。這證明σ是單射，還可以證明σ是滿射，因而σ是雙射，把σ的逆變換記為，易見也是正交變換。
性質6 正交變換把平行直線變成平行直線。
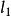平面正交變換
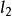平面正交變換
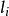平面正交變換
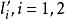平面正交變換
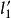平面正交變換
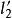平面正交變換
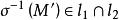平面正交變換 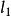平面正交變換 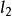平面正交變換 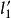平面正交變換 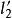平面正交變換證：設σ是正交變換，設∥，由性質4，σ把直線變成直線，如果與交於M'，則，這與∥矛盾，所以∥。
性質7 正交變換保持向量長度與夾角。
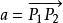平面正交變換
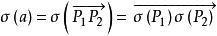平面正交變換證： 設向量，定義，易見性質7成立。
性質8 正交變換把平面直角坐標系變成平面直角坐標系。
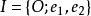平面正交變換
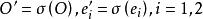平面正交變換
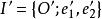平面正交變換證： 設為平面直角坐標系，σ為正交變換，記，則為平面直角坐標系(由性質7)。
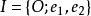平面正交變換 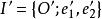平面正交變換定理1 設正交變換σ把直角標架變成直角標架，其中，
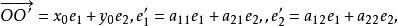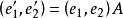平面正交變換
平面正交變換
平面正交變換即，則σ在直角坐標系中的表示是
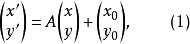平面正交變換
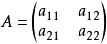平面正交變換其中是正交矩陣。
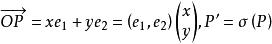平面正交變換
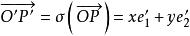平面正交變換證： 設，則，設
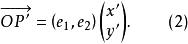平面正交變換由
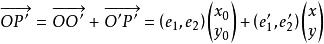平面正交變換
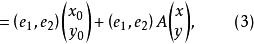平面正交變換結合(2)與(3)，就得到(1)。
註：（1）表示平面上的平移，旋轉反射或它們的複合 。
