機率數論

機率數論是研究數論函式的分布問題。機率數論開始於1917年G.H.哈代與S.A.拉馬努金關於數論函式ω(n)的研究。

機率數論

正文

研究數論函式的分布問題。機率數論開始於1917年G.H.哈代與S.A.拉馬努金關於數論函式ω(n)的研究。此處ω(n)表示n的不同素因子的個數,例如ω(1)=0,ω(2)=1，ω(20)=2,ω(30)=3。對於任意的k,當n為k個不同素數之積時,有ω(n)=k。特別,當n=p為素數時,有ω(p)=1。所以ω(n)(n=1,2,…)的分布很不規則，它可以取任意大的整數值,而又無窮多次取值1及2,3等。因此,研究ω(n)的值分布就從研究ω(n)在區間【1,x】中的期望值入手,其中x是大於或等於2的整數。命Ak表示區間【1,x】中為k所整除的整數組成的集合,Px(Ak)表示Ak的機率。例如當x=100時，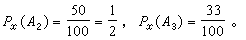

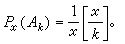
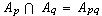一般說來

假定p、q為互異的素數，則，所以當x充分大時，有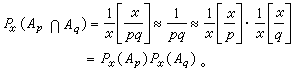

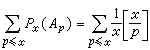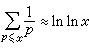這說明當n在區間【1,x】中隨機選取時，事件Ap與Aq是漸近獨立的，所以ω(n)在【1,x】中的期望值為

，

它漸近地等於（見素數分布）。
命ψ(y)為任何當y趨於無窮時亦趨於無窮的函式,則。
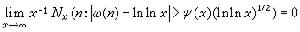這就說明在 ω(n)(1≤n≤x)中，只有極少數是偏離ln lnx 的。
1934年，P.圖蘭進而證明了

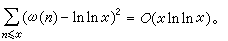
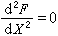1939年P.愛爾特希與M.卡茨發展了P.圖蘭的方法，證明了中心極限定理: 命ƒ(n)為適合│ƒ(p)│≤1 的強加性函式。所謂強加性函式，即當(m ,n)=1時,ƒ（m ,n）=ƒ(m)+ƒ(n),且又命。假定B(x)→∞（當x→∞時），則

,

並稱之為愛爾特希-卡茨定理。
當取ƒ(n)=ω(n)，則得

在機率數論方面作過重要貢獻的還有J.庫比利烏斯、M.B.巴班、A.溫特納和P.D.T.A.埃利奧特等人。
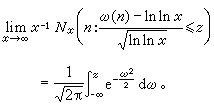
參考書目
　P.D.T.A.Elliott,Probabilistic Number Theory,Ⅰ,Ⅱ,ASer.Comp.Stu.Math.,Spr.Ver.,No.239,240,1980.

配圖

相關連線