樹分類器
正文
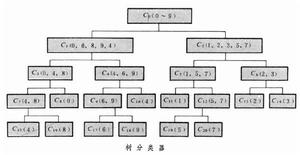需要通過多級判別才能確定模式所屬類別的一種分類方法。多級判別過程可以用樹狀結構表示，所以稱為樹分類器。例如在對0～9十個數字進行識別時，可以先根據某些特徵把0，6，8，9，4分成一類（C1）,把1，2，3，5，7分成一類(C2),然後根據這些特徵或另外一些特徵把0，6，8，9，4這一類再分成0，4，8一類 (C3)和4，6，9一類(C4)等，直到最後把各個數字分開為止（見圖）。這種樹狀結構由節點和樹枝所組成，它的特點是除了樹根C0沒有前級節點(父節點)以外，其餘節點都有唯一的父節點（例如C的父節點是C,且所有的節點都可以從樹根沿樹枝所組成的路徑達到。沒有後繼節點（子節點）的節點叫作葉，如C8，C10，C11等，其餘的叫作非終止節點。每個非終止節點都只有兩個子節點的樹分類器，是最常用的一類樹分類器，稱為二分樹分類器。 每個終止節點對應一個類別，為了提高樹分類器的正確識別率，允許有幾個葉對應同一個類別。非終止節點對應的類別是它的子節點所對應的類別的總和。
樹分類器的設計需要解決以下幾個問題：
① 確定樹的結構。樹結構影響正確識別率和平均判別次數，一般根據所研究問題的性質確定某種與正確識別率有聯繫的目標函式代替正確識別率，作為判斷結構是否合理的標準，從樹根出發在每個非終止節點尋找使目標函式達到最小（或最大）的子節點和對應的類別配置。
② 對每個非終止節點選擇用於判別的特徵子集，分枝限界算法能提供選擇最佳特徵子集的有效方法。
③ 為每個非終止節點確定判別函式，最常用的判別函式是線性判別函式。
由於在每個非終止節點需要判別的類別比較少，在多數情況下,可以用較少的特徵和較簡單的判別函式(因而較少的計算機時間)以達到總體上比較好的分類效果。
