基本概念
模糊邏輯是建立在多值邏輯基礎上，運用模糊集合的方法來研究模糊性思維、語言形式及其規律的科學。模糊邏輯控制(Fuzzy Logic Control)這一概念1974年由L.A.Zadeh教授提出。其核心是對複雜的系統或過程建立一種語言分析的數學模式，使自然語言能直接轉化為計算機所能接受的算法語言。
模糊邏輯原理
模糊邏輯指模仿人腦的不確定性概念判斷、推理思維方式，對於模型未知或不能確定的描述系統，以及強非線性、大滯後的控制對象，套用模糊集合和模糊規則進行推理，表達過渡性界限或定性知識經驗，模擬人腦方式，實行模糊綜合判斷，推理解決常規方法難於對付的規則型模糊信息問題。模糊邏輯善於表達界限不清晰的定性知識與經驗，它藉助於隸屬度函式概念，區分模糊集合，處理模糊關係，模擬人腦實施規則型推理，解決因“排中律”的邏輯破缺產生的種種不確定問題 。
模糊邏輯與計算機結合形成的Fuzzy控制系統為計算機模擬人腦實現複雜控制提供一條途徑。Fuzzy控制的基本特徵是利用人的經驗、知識和推理技術以及控制系統提供的狀態條件信息，而不依賴物理過程的精確數學模型，因此簡化了複雜的控制問題。
實際上，模糊邏輯是把多值邏輯、機率論、人工智慧和神經網路結合在一起，是一門具有堅實的數學理論基礎的控方法論，用體現在客觀物理系統中的固有印象來仿真人的思維推理。
模糊系統根據語擊變數形式的輸入做出判斷，因為人類是利用語言考慮事物的，變數用少量的IF-THEN(如果/則)規則來測試，根據所採用的規則產生一個或多個回響If描述控制對象的概念，THEN描述由概念作出的操作。每個規則的回響根據其輸入的置信度或從屬度加權，計算回響曲線以產生適當的輸出。模糊邏輯藉助人工智慧的If-Then結構，但不想人工智慧能那樣複雜，而又使用少數的規則。神經網路類似模糊邏輯，但它對每一個刺激分配分立的權，而模糊邏輯是一個連續數值狀態的系統 。
模糊控制器
模糊控制是以模糊集合理論、模糊語言及模糊邏輯為基礎的控制，它是模糊數學在控制系統中的套用，是一種非線性智慧型控制。模糊控制是利用人的知識對控制對象進行控制的一種方法，通常用“if條件，then結果”的形式來表現，所以又通俗地稱為語言控制。一般用於無法以嚴密的數學表示的控制對象模型，即可利用人（熟練專家）的經驗和知識來很好地控制。因此利用人的智力模糊地進行系統控制的方法就是模糊控制 。
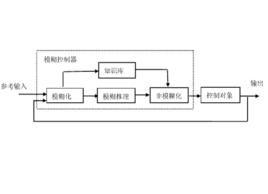
如圖1所示，模糊控制器的基本結構包括知識庫、模糊推理、輸入量模糊化、輸出量精確化四部分。
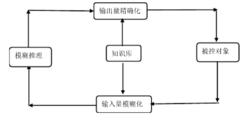模糊邏輯過程控制圖1
（1）知識庫
知識庫包括模糊控制器參數庫和模糊控制規則庫。模糊控制規則建立在語言變數的基礎上。語言變數取值為“大”、“中”、“小”等這樣的模糊子集，各模糊子集以隸屬函式表明基本論域上的精確值屬於該模糊子集的程度。因此，為建立模糊控制規則，需要將基本論域上的精確值依據隸屬函式歸併到各模糊子集中，從而用語言變數值(大、中、小等)代替精確值。這個過程代表了人在控制過程中對觀察到的變數和控制量的模糊劃分。由於各變數取值範圍各異，故首先將各基本論域分別以不同的對應關係，映射到一個標準化論域上。通常，對應關係取為量化因子。為便於處理，將標準論域等分離散化，然後對論域進行模糊劃分，定義模糊子集，如NB、PZ、PS等。
同一個模糊控制規則庫，對基本論域的模糊劃分不同，控制效果也不同。具體來說，對應關係、標準論域、模糊子集數以及各模糊子集的隸屬函式都對控制效果有很大影響。這3類參數與模糊控制規則具有同樣的重要性，因此把它們歸併為模糊控制器的參數庫，與模糊控制規則庫共同組成知識庫。
（2）模糊化
將精確的輸入量轉化為模糊量F有兩種方法:
a.將精確量轉換為標準論域上的模糊單點集。
精確量x經對應關係G轉換為標準論域x上的基本元素.
b.將精確量轉換為標準論域上的模糊子集。
精確量經對應關係轉換為標準論域上的基本元素，在該元素上具有最大隸屬度的模糊子集，即為該精確量對應的模糊子集。
（3）模糊推理
最基本的模糊推理形式為:
前提1 IF A THEN B
前提2 IF A′
結論 THEN B′
其中，A、A′為論域U上的模糊子集，B、B′為論域V上的模糊子集。前提1稱為模糊蘊涵關係，記為A→B。在實際套用中，一般先針對各條規則進行推理，然後將各個推理結果總合而得到最終推理結果。
（4）精確化
推理得到的模糊子集要轉換為精確值，以得到最終控制量輸出y。目前常用兩種精確化方法：
a.最大隸屬度法。在推理得到的模糊子集中，選取隸屬度最大的標準論域元素的平均值作為精確化結果。
b.重心法。將推理得到的模糊子集的隸屬函式與橫坐標所圍面積的重心所對應的標準論域元素作為精確化結果。在得到推理結果精確值之後，還應按對應關係，得到最終控制量輸出y。
意義
模糊控制擁有很多的優勢，比如簡化系統設計的複雜性，特別適用於非線性、時變、模型不完全的系統上。模糊控制技術利用控制法則來描述系統變數間的關係。同時不用數值而用語言式的模糊變數來描述系統，模糊控制器不必對被控制對象建立完整的數學模式。模糊控制器是一語言控制器，使得操作人員易於使用自然語言進行人機對話。模糊控制器是一種容易控制、掌握的較理想的非線性控制器，並且抗干擾能力強，回響速度快，並對系統參數的變化有較強的魯棒性和較佳的容錯性。最後它是從屬於智慧型控制的範疇。該系統尤其適於非線性，時變，滯後系統的控制 。
（1）運用模糊邏輯變數、模糊邏輯函式和似然推理等新思想、新理論，為尋找解決模糊性問題的突破口奠定了理論基礎，從邏輯思想上為研究模糊性對象指明了方向。
（2）模糊邏輯在原有的布爾代數、二值邏輯等數學和邏輯工具難以描述和處理的自動控制過程、疑難病症的診斷、大系統的研究等方面，都具有獨到之處。
（3）在方法論上，為人類從精確性到模糊性、從確定性到不確定性的研究提供了正確的研究方法。
此外，在數學基礎研究方面，模糊邏輯有助於解決某些悖論。對辯證邏輯的研究也會產生深遠的影響。當然，模糊邏輯理論本身還有待進一步系統化、完整化、規範化。
