簡介
基本內容
模糊邏輯指模仿人腦的不確定性概念判斷、推理思維方式，對於模型未知或不能確定的描述系統，以及強非線性、大滯後的控制對象，套用模糊集合和模糊規則進行推理，表達過渡性界限或定性知識經驗，模擬人腦方式，實行模糊綜合判斷，推理解決常規方法難於對付的規則型模糊信息問題。模糊邏輯善於表達界限不清晰的定性知識與經驗，它藉助於隸屬度函式概念，區分模糊集合，處理模糊關係，模擬人腦實施規則型推理，解決因“排中律”的邏輯破缺產生的種種不確定問題 。
歷史發展
1965年美國數學家L. Zadeh首先提出了Fuzzy集合的概念，標誌著Fuzzy數學的誕生。建立在二值邏輯基礎上的原有的邏輯與數學難以描述和處理現實世界中許多模糊性的對象。Fuzzy數學與Fuzzy邏輯實質上是要對模糊性對象進行精確的描述和處理。L. Zadeh為了建立模糊性對象的數學模型，把只取0和1二值的普通集合概念推廣為在[0，1]區間上取無窮多值的模糊集合概念，並用“隸屬度”這一概念來精確地刻畫元素與模糊集合之間的關係。正因為模糊集合是以連續的無窮多值為依據的，所以，模糊邏輯可看做是運用無窮連續值的模糊集合去研究模糊性對象的科學。把模糊數學的一些基本概念和方法運用到邏輯領域中，產生了模糊邏輯變數、模糊邏輯函式等基本概念。對於模糊聯結詞與模糊真值表也作了相應的對比研究。查德還開展了模糊假言推理等似然推理的研究，有些成果已直接套用於模糊控制器的研製。創立和研究模糊邏輯的主要意義有：（1）運用模糊邏輯變數、模糊邏輯函式和似然推理等新思想、新理論，為尋找解決模糊性問題的突破口奠定了理論基礎，從邏輯思想上為研究模糊性對象指明了方向。（2）模糊邏輯在原有的布爾代數、二值邏輯等數學和邏輯工具難以描述和處理的自動控制過程、疑難病症的診斷、大系統的研究等方面，都具有獨到之處。（3）在方法論上，為人類從精確性到模糊性、從確定性到不確定性的研究提供了正確的研究方法。此外，在數學基礎研究方面，模糊邏輯有助於解決某些悖論。對辯證邏輯的研究也會產生深遠的影響。當然，模糊邏輯理論本身還有待進一步系統化、完整化、規範化。
基本理論
模糊邏輯是二元邏輯的重言式：在多值邏輯中，給定一個 MV-代數A，一個 A-求值就是從命題演算中公式的集合到 MV-代數的函式。如果對於所有 A-求值這個函式把一個公式映射到 1（或 0），則這個公式是一個 A-重言式。因此對於無窮值邏輯（比如模糊邏輯、武卡謝維奇邏輯），我們設 [0,1] 是 A 的下層集合來獲得 [0,1]-求值和 [0,1]-重言式（經常就叫做求值和重言式）。Chang 發明 MV-代數來研究波蘭數學家揚·武卡謝維奇（Jan ?ukasiewicz）在 1920 年介入的多值邏輯。Chang 的完備定理(1958, 1959) 聲稱任何在 [0,1] 區間成立的 MV-代數等式也在所有 MV-代數中成立。通過這個定理，證明了無窮值的武卡謝維奇邏輯可以被 MV-代數所刻畫。後來同樣適用於模糊邏輯。這類似於在 {0,1} 成立的布爾代數等式在任何布爾代數中也成立，布爾代數因此刻畫了標準二值邏輯。
套用
模糊邏輯可以用於控制家用電器比如洗衣機(它感知裝載量和清潔劑濃度並據此調整它們的洗滌周期)和空調。
基本的套用可以特徵化為連續變數的子範圍(subranges)，形狀常常是三角形或梯形。例如，防鎖剎車的溫度測量可以有正確控制剎車所需要的定義特定溫度範圍的多個獨立的成員關係函式（歸屬函式 / Membership function）。每個函式映射相同的溫度到在 0 至 1 範圍內的一個真值且為非凹函式(non-concave functions)（否則可能在某部分溫度越高卻被歸類為越冷）。接著這些真值可以用於確定應當怎樣控制剎車。
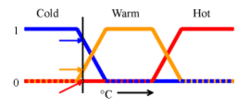一個溫度控制的例子在右圖中，冷、暖和熱是映射溫度範圍的函式。在這個刻度上的一個點有三個"真值" — 每個函式一個。對於展示的特定的溫度，這三個真值可以被解釋為把溫度描述為，"相當冷", "有些暖" 和 "不熱"。
通常情況會採用梯形，但在作模糊回歸分析時則會選用三角形的歸屬函式。
模糊邏輯模糊邏輯通常使用 IF/THEN 規則，或構造等價的東西比如模糊關聯矩陣。
規則通常表達為如下形式:
IF 模糊變數 IS模糊集合THEN動作
例如，一個非常簡單的使用風扇的溫度調節器:
IF 溫度 IS 非常冷 THEN 停止風扇
IF 溫度 IS 冷 THEN 減速風扇
IF 溫度 IS 正常 THEN 保持現有水平
IF 溫度 IS 熱 THEN 加速風扇
注意沒有 "ELSE"。所有規則都被求值，因為溫度在不同程度上可以同時是"冷"和"正常"。
在模糊邏輯中存在著布爾邏輯的 AND、OR 和 NOT運算符，它們通常定義為最小、最大和求補；在以這種方式定義它們的時候，它們叫做Zadeh 運算符，因為它們是在 Zadeh 最初論文中首次定義的。對於模糊變數 x 和 y:
NOT x = (1 - truth(x))x AND y = minimum(truth(x), truth(y))x OR y = maximum(truth(x), truth(y))還可以套用叫做hedges的更貼近自然語言其他的運算符。一般性的副詞如"非常"或"有點"能使用數學公式修改集合的內涵。
程式語言
在套用中，程式語言 ProLog 由於有架設被演繹邏輯問訊的"規則"的資料庫設施而很適合實現模糊邏輯。這種編程叫做邏輯編程。
其他例子
如果一個人的高度是 1.8 米，把他考慮為高:
IF male IS true AND height >= 1.8 THEN is_tall IS true
IF male IS true AND height >= 1.8 THEN is_short IS false
但上述的定義卻是不現實的。因此，在模糊規則下，在高和矮之間不做明顯的區分:
IF height >= medium male THEN is_short IS agree somehow
IF height >= medium male THEN is_tall IS agree somehow
在模糊的情況下，沒有像 1,83 米這樣的高度，只有模糊值，比如下列賦值:
dwarf male = [0, 1.3]
msmall male = (1.3, 1.5]
medium male = (1.5, 1.8]
tall male = (1.8, 2.0]
giant male > 2.0 m對於結論，也不只是兩個值，而是五個:
agree not = 0
agree little = 1
agree somehow = 2
agree alot = 3
agree fully = 4
在二值或"脆弱"的情況下，高度為 1.79 米的一個人可能被認為是矮。如果另一個人的高度是 1.8 米或 2.25 米，這些人才被當作是高。
這個脆弱的例子故意的區別於模糊的例子。我們在前提中不能放置
IF male >= agree somehow AND ...因為性別經常被認為是二值信息。所以不象身高這么複雜。
