簡介
傾向評分匹配（Propensity Score Matching，簡稱PSM）是一種統計學方法，用於處理觀察研究（Observational Study）的數據。在觀察研究中，由於種種原因，數據偏差（bias）和混雜變數（confounding variable）較多，傾向評分匹配的方法正是為了減少這些偏差和混雜變數的影響，以便對實驗組和對照組進行更合理的比較。這種方法最早由Paul Rosenbaum和Donald Rubin在1983年提出，一般常用於醫學、公共衛生、經濟學等領域。 以公共衛生學為例，假設研究問題是吸菸對於大眾健康的影響，研究人員常常得到的數據是觀察研究數據，而不是隨機對照實驗數據（Randomized Controlled Trial data），因為吸菸者的行為和結果，以及不吸菸者的行為和結果，是很容易觀察到的。但如果要進行隨機對照實驗，招收大量被試，然後隨機分配到吸菸組和不吸菸組，這種實驗設計不太容易實現，也並不符合科研倫理。這種情況下觀察研究是最合適的研究方法。但是面對最容易獲得的觀察研究數據，如果不加調整，很容易獲得錯誤的結論，比如拿吸菸組健康狀況最好的一些人和不吸菸組健康狀況最不好的一些人作對比，得出吸菸對於健康並無負面影響的結論。從統計學角度分析原因，這是因為觀察研究並未採用隨機分組的方法，無法基於大數定理的作用，在實驗組和對照組之間削弱混雜變數的影響，很容易產生系統性的偏差。傾向評分匹配就是用來解決這個問題，消除組別之間的干擾因素。
PSM介紹
而“反事實”的推斷法則是：如果沒有A，那么B的結果將怎樣（此時，其實A已經發生了）？因此，對於處在干預狀態(treatment condition)的成員而言，反事實就是處在控制狀態(condition of control)下的潛在結果(potential outcome)；相反，對於處在控制狀態的成員而言，反事實就是處在干預狀態下的潛在結果。顯然，這些潛在結果是我們無法觀測到的，也就是說，它們是缺失的。
傾向評分匹配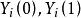
傾向評分匹配
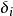傾向評分匹配我們假定有N個個體，每一個處在干預中的個體i（i=1,2, ,N）都將有兩種潛在結果（ ），分別對應著未被干預狀態和干預狀態中的潛在結果。那么對一個個體進行干預的效應標記為 ，表示干預狀態的潛在結果與未干預狀態的潛在結果之間的差，即：
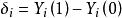傾向評分匹配
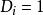傾向評分匹配
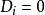傾向評分匹配
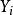傾向評分匹配令 表示接受干預， 表示未接受干預，同時 表示所測試的結果變數。那么反事實框架可以表示為以下模型：
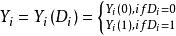傾向評分匹配該模型也可以表示為：
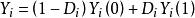傾向評分匹配這個模型表明，兩種結果中的哪一種將在現實中被觀測到，取決於干預狀態，即D的狀態。
用ATT(Average treatmenteffect for the treated)來測度個體在干預狀態下的平均干預效應，即表示個體i在干預狀態下的觀測結果與其反事實的差，稱為平均干預效應的標準估計量，
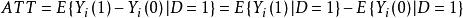傾向評分匹配
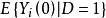傾向評分匹配
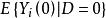傾向評分匹配很明顯，反事實 是我們觀測不到的，所以我們只有使用個體i在未干預狀態下的觀測結果 作為替代來估計個體在干預狀態下的潛在結果——反事實。所以，給公式可以進一步表示為：
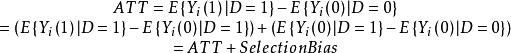傾向評分匹配 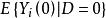傾向評分匹配 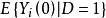傾向評分匹配顯然，這裡需要到數據的隨機性了。在實驗數據中，個體是隨機分配(random assignment)的，所以個體的所有特徵在干預組和控制組之間是相等，也就無需考慮用 作為替代對反事實 進行估計時存在的偏差了，這裡稱為選擇偏倚，換句話說，實驗數據能夠確保數據的選擇偏倚為0，所以實驗設計中，隨機性能保證干預組和控制組之間的數據平衡。而對於觀測數據，往往由於缺乏隨機性，而導致干預組和控制組不僅僅在干預統計量上存在不同，還在第三方變數X（這個變數是可觀測的）上存在區別。這時，我們必須要考慮到這些區別以防止出現潛在偏倚。
這時就要採用匹配的方式進行干預效應分析。匹配的目的在於確保干預效應估計是建立在可比個體之間的不同結果的基礎上。最簡單的匹配方式是將干預組和控制組中第三方變數X的值相同的兩個個體進行配對分析。但是，如果X並不是某一個變數，而是一組變數時，最終簡單的匹配方式也就不再適用，而是採用傾向得分匹配方式進行匹配。
最簡單匹配方法的幾個假設：
條件獨立假設(conditionalindependence assumption or CIA)：給定X後干預狀態的潛在結果是獨立的，換句話說，控制住X之後，干預分配就相當於隨機分配。
共同支撐條件(common support condition)：
對於X的每一個值，存在於干預組或控制組的可能性均為正，即
1.條件獨立假設(conditionalindependence assumption or CIA)：給定X後干預狀態的潛在結果是獨立的，換句話說，控制住X之後，干預分配就相當於隨機分配。
2.共同支撐條件(common support condition)：
對於X的每一個值，存在於干預組或控制組的可能性均為正，即
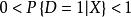傾向評分匹配。
同時，第二個要求稱為覆蓋條件，即匹配組變數X需要在干預組和控制組上有足夠的覆蓋，即處理組每一個個體在控制組中都能找到與之匹配的X。
若X只有一個變數，則對於給定的X=x，ATT(x)的表達式為：
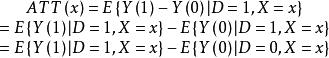傾向評分匹配顯然，X只有一個變數時，干預組和控制組針對X的匹配標準是清晰的：對於干預組個體和控制組個體，他們的X變數的值越近，這兩個個體的特徵也就越相似。
但，如果X不再只是一個變數，而是一組變數時，所謂“近”的判斷標準也就變得模糊起來。針對這個問題，Rosenbaum and Rubin (1983)解決了維度問題，並證明了如果基於X相關變數的匹配是有效的，那么基於X變數組的傾向得分的匹配也將同樣有效，從而奠定了PSM的理論基礎。
這裡，傾向得分是通過logist回歸獲得的，從而將X由多維降到了一維的水平。所以傾向得分中包含了X中所有變數的信息，綜合反映了每個個體X變數組的水平。顯然，傾向得分匹配的優勢很明顯——降維，它由單個變數（傾向得分）對個體進行匹配來代替了X所有變數為基礎對個體進行匹配。
同樣的，PSM的主要定理總結為以下幾點：
定理一，傾向得分p(X)是一個平衡得分。有著相同傾向得分的兩組個體之間的特徵顯然是平衡的。
定理二，如果條件獨立假設依舊成立，那么潛在結果在傾向得分的條件下也將獨立於干預狀態。也就是說，只要向量X包含滿足CIA的所有相關信息，那么傾向得分的條件作用也就等價於向量X中所有變數的條件作用。
所以，PSM的ATT(x)的表達式為：
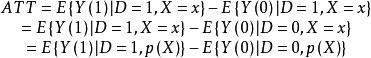傾向評分匹配為了估計ATT，需對p(X)在干預上的條件作用的分布取平均：
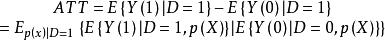傾向評分匹配PSM的步驟
計算傾向值（採用logistic回歸）
進行得分匹配
得分匹配的幾種方法：
（1）最鄰近匹配（Nearest neighbor matching, NNM）(是否使用卡尺 with or without caliper)
以傾向得分為依據，在控制組樣本中向前或向後尋找最接近干預組樣本得分的對象，並形成配對。
（2）半徑匹配（Radius matching）
設定一個常數r（可理解為區間或範圍，一般設定為小於傾向得分標準差的四分之一），將實驗組中得分值與控制組得分值的差異在r內的進行配對。
（3）核匹配（Kernel Matching）
將干預組樣本與由控制組所有樣本計算出的一個估計效果進行配對，其中估計效果由實驗組個體得分值與控制組所有樣本得分值加權平均獲得，而權數則由核函式計算得出。
評定匹配後的平衡性
計算平均干預效果（ATT）
進行敏感性分析
1.計算傾向值（採用logistic回歸）
2.進行得分匹配
得分匹配的幾種方法：
（1）最鄰近匹配（Nearest neighbor matching, NNM）(是否使用卡尺 with or without caliper)
以傾向得分為依據，在控制組樣本中向前或向後尋找最接近干預組樣本得分的對象，並形成配對。
（2）半徑匹配（Radius matching）
設定一個常數r（可理解為區間或範圍，一般設定為小於傾向得分標準差的四分之一），將實驗組中得分值與控制組得分值的差異在r內的進行配對。
（3）核匹配（Kernel Matching）
將干預組樣本與由控制組所有樣本計算出的一個估計效果進行配對，其中估計效果由實驗組個體得分值與控制組所有樣本得分值加權平均獲得，而權數則由核函式計算得出。
3.評定匹配後的平衡性
4.計算平均干預效果（ATT）
5.進行敏感性分析
適用情形
傾向評分匹配法適用於兩類情形。 第一，在觀察研究中，對照組與實驗組中可直接比較的個體數量很少。在這種情形下，實驗組和對照組的交集很小，比如治療組健康狀況最好的10%人群與非治療組健康狀況最差的10%人群是相似的，如果將這兩個重合的子集進行比較，就會得出非常偏倚的結論。 第二，由於衡量個體特徵的參數很多，所以想從對照組中選出一個跟實驗組在各項參數上都相同或相近的子集作對比變得非常困難。在一般的匹配方法中，我們只需要控制一兩個變數（如年齡、性別等）即可，就可以很容易從對照組中選出一個擁有相同特徵的子集，以便與實驗組進行對比。但是在某型情形下，衡量個體特徵的變數會非常多，這時想選出一個理想的子集變得非常困難。經常出現的情形是，控制了某些變數，但是在其他變數上差異很大，以至於無法將實驗組和對照組進行比較。
傾向評分匹配通過使用邏輯回歸模型來決定評分。
