施托爾茨極限定理

施托爾茨極限定理是給出求極限的一種方法的命題。施托爾茨極限定理對函式極限也可得出類似結論。

簡介

施托爾茨極限定理是給出求極限的一種方法的命題。 該定理斷言：

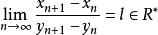施托爾茨極限定理

若，且滿足下列條件中的一個：

1、{y}嚴格增，y→+∞（或{y}嚴格減）

2、x→0，y→0，{y}嚴格減

則

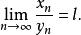施托爾茨極限定理

對函式極限的結論

施托爾茨極限定理對函式極限的類似結論如下：

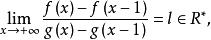施托爾茨極限定理

設f:(a,+∞)→R在任意有限區間(a,b)內有界；當x→+∞時，g(x)→+∞，且g(x)嚴格單調增，若則

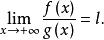施托爾茨極限定理

函式極限

函式極限是高等數學最基本的概念之一，導數等概念都是在函式極限的定義上完成的。

函式極限性質的合理運用。常用的函式極限的性質有函式極限的唯一性、局部有界性、保序性以及函式極限的運算法則和複合函式的極限等等。