定義
 極大無關組
極大無關組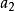 極大無關組
極大無關組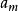 極大無關組
極大無關組 極大無關組
極大無關組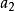 極大無關組
極大無關組 極大無關組
極大無關組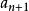 極大無關組
極大無關組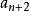 極大無關組
極大無關組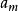 極大無關組
極大無關組 極大無關組
極大無關組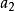 極大無關組
極大無關組 極大無關組
極大無關組 極大無關組
極大無關組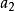 極大無關組
極大無關組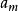 極大無關組
極大無關組設 , ,..., 是數域P上線性空間V的一個向量組,如果其部分向量組 , ,..., 線性無關(其中m>n),且每個 , ,..., 都可由它線性表出,則稱 , ,..., 是向量組 , ,..., 的一個極大無關組 。
性質
任何向量組都與其極大無關組等價;一個向量組的任意兩個極大無關組所含向量個數是相同的。
 極大無關組
極大無關組 極大無關組
極大無關組 極大無關組
極大無關組 極大無關組
極大無關組 極大無關組
極大無關組 極大無關組
極大無關組 極大無關組
極大無關組 極大無關組
極大無關組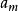 極大無關組
極大無關組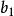 極大無關組
極大無關組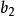 極大無關組
極大無關組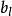 極大無關組
極大無關組 極大無關組
極大無關組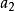 極大無關組
極大無關組 極大無關組
極大無關組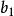 極大無關組
極大無關組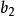 極大無關組
極大無關組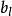 極大無關組
極大無關組若向量組,,...,的極大無關組含有r個向量,則稱r為此向量組的秩,記為r(,,...,)。全為零向量的向量組是惟一沒有極大無關組的向量組,規定其秩為零。若向量組,,...,可由向量組,,...,線性表出,則,,...,可以線性表示,,...,。若兩個向量組等價,則它們有相同的秩。極大無關組的概念可以推廣到含無限個向量的情形。因此,線性空間V的任一個基可看成V的極大無關組。特別的,齊次線性方程組的基礎解系是其解空間的極大無關組 。

