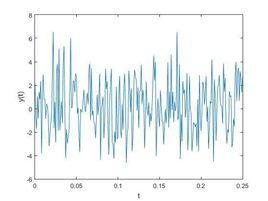
簡介
梅爾倒頻譜係數(Mel-Frequency Cipstal Coefficients, MFCC)是一組用來建立梅爾倒頻譜的關鍵係數。由音樂訊號當中的片段,我們可以得到一組足以代表此音樂訊號之倒頻譜,而梅爾倒頻譜係數即是從這個倒頻譜中推得的倒頻譜(也就是頻譜的頻譜)。與一般的倒頻譜不同 ,梅爾倒頻譜最大的特色在於,於梅爾倒頻譜上的頻帶是均勻分布於梅爾刻度上的,也就是說,這樣的頻帶會較一般我們所看到、線性的倒頻譜表示方法,和人類非線性的聽覺系統(audio system)更為接近。例如:我們在音訊壓縮的技術中,便常常使用梅爾倒頻譜來處理。
梅爾倒頻譜係數通常是用以下方法得到的:
將一訊號進行傅立葉轉換(Fourier transform)
將頻譜映射(mapping)至梅爾刻度,利用三角窗函式(triangular overlapping window)
取對數(logarithm)
取離散餘弦轉換(discrete cosine transform)
MFCC是轉換後的頻譜
1.將一訊號進行傅立葉轉換(Fourier transform)
2.將頻譜映射(mapping)至梅爾刻度,利用三角窗函式(triangular overlapping window)
3.取對數(logarithm)
4.取離散餘弦轉換(discrete cosine transform)
5.MFCC是轉換後的頻譜
取得梅爾倒頻譜的方法眾多,上述只是其中一種。
另外,ETSI在2000年左右有定義一套專為行動電話設計的梅爾倒頻譜係數算法。
套用
梅爾倒頻譜係數通常可以用於作為語音辨識(speech recognition)系統中的特徵質觀察,例如:可以自動辨認一個人透過電話說的數字。梅爾倒頻譜係數通常也可以作為聲文辨識(Speaker Recognition),也就是、用來辨識某段語音訊號的發話者是誰的技術。
梅爾倒頻譜係數在近年來於音樂分類(music genre classification)相關套用的領域也逐漸嶄露頭角,例如尋找一段音樂的相似程度等。
語音辨識
梅爾頻率倒譜係數MFCC和感知線性預測PLP:不同於LPC等通過對人的發聲機理的研究而得到的聲學特徵,Mel倒譜係數MFCC和感知線性預測PLP是受人的聽覺系統研究成果推動而導出的聲學特徵。對人的聽覺機理的研究發現,當兩個頻率相近的音調同時發出時,人只能聽到一個音調。臨界頻寬指的就是這樣一種令人的主觀感覺發生突變的頻寬邊界,當兩個音調的頻率差小於臨界頻寬時,人就會把兩個音調聽成一個,這稱之為禁止效應。Mel刻度是對這一臨界頻寬的度量方法之一。 MFCC的計算首先用FFT將時域信號轉化成頻域,之後對其對數能量譜用依照Mel刻度分布的三角濾波器組進行卷積,最後對各個濾波器的輸出構成的向量進行離散餘弦變換DCT,取前N個係數。PLP仍用德賓法去計算LPC參數,但在計算自相關參數時用的也是對聽覺激勵的對數能量譜進行DCT的方法。
噪聲
梅爾倒頻譜係數並非相當穩定,在計算當中,一組係數其實相當容易受到外加的噪聲影響;為了對抗噪聲,我們通常會將梅爾倒頻譜係數在語音辨認上進行正規化(normalization)的動作,以減少噪聲造成的影響。
另外,有些研究者會將梅爾倒頻譜係數基礎的算法設計的更加頑強,例如:在進行餘弦轉換前增加對數化梅爾係數的能量值至一個合適的範圍,以減少諸如噪聲等低能量項對於整個係數結果的影響。
歷史
一般認為Paul Mermelstein是主要致力於發展梅爾倒頻譜的人,然而 Mermelstein 本人卻將主要的概念功勞歸給 Bridle 和 Brownfor the idea:
Bridle 和 Brown 運用了一組十九個、由余弦轉換導出的頻譜型的係數,轉換的輸入值是訊號在一組在頻帶上有非均勻間隔分布的帶通濾波器(band pass)後的輸出。
濾波器的間隔是呈現對數分布的;因此,我們一般稱之為梅爾式的導頻譜係數
通常此兩組起源都會被人當作參照使用。
另外,許多作者包括Mermelstein都認為,梅爾倒頻譜中這樣以頻譜為基準的餘弦轉換函式,非常接近早期用於語音表征和辨認、對對數化頻譜進型的主成分分析;關於這部分相關的資訊,可參考Pols和它同事的研究。
係數推導
1. 對該信號做傅立葉變換
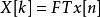 梅爾倒頻譜
梅爾倒頻譜2. 根據下面公式算出Y[m]
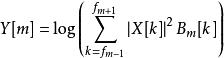 梅爾倒頻譜
梅爾倒頻譜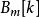 梅爾倒頻譜
梅爾倒頻譜其中
是梅爾頻率倒頻譜的遮罩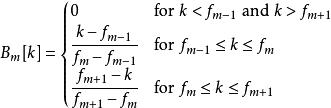 梅爾倒頻譜
梅爾倒頻譜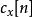 梅爾倒頻譜
梅爾倒頻譜3.對Y[m]做IDCT得,因為Y[m]是偶函式,故用IDCT(反離散餘弦變換)取代IDFT(反離散傅立葉變換)
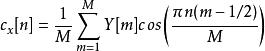 梅爾倒頻譜
梅爾倒頻譜