格泰特法則
正文
關於繞飛行器或其部件的可壓縮氣體流動的普遍變換規律,適用於能夠用線性位流方程(見計算空氣動力學)描述的問題,即小迎角薄翼和細長機身的來流馬赫數不接近於 1的繞流問題。這一法則是德國流體力學家B.格泰特於1941年提出的,可用來研究空氣壓縮性或來流馬赫數M∞對物體空氣動力特性的影響。對於同一類機翼或機身,在表示M∞和幾何參數對壓強分布和空氣動力特性的影響時,利用這一法則提供的組合參數可以減少獨立變數的數目,因而廣泛套用于歸納繪製理論與實驗結果的圖線。法則的具體內容是:在亞音速可壓縮流動中有一機翼或機身,取x軸沿迎面來流方向,z軸沿翼平面展向,y軸指向上方。如果在另一不可壓縮流動(M∞=0)中,有一對應機翼或機身,其x方向尺寸與可壓縮流動中的機翼或機身相同,而y方向與z方向的尺寸縮為可壓縮流動中的β倍(
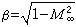 ),則可壓縮流動中的壓強係數 Cp(見卡門-錢學森公式)與不可壓縮流動中對應點的壓強係數 Cp0之間存在比例關係:
),則可壓縮流動中的壓強係數 Cp(見卡門-錢學森公式)與不可壓縮流動中對應點的壓強係數 Cp0之間存在比例關係: 
對於扁平薄翼繞流問題,線上性小擾動理論的近似範圍內還有更簡單的法則。也即在確定不可壓縮流動中的對應機翼時,可保持y方向的尺寸也不變,而其他兩方向仍按格泰特法則的規定。因而可壓縮與不可壓縮流場中兩機翼的平面形狀不同,但迎角與相對厚度保持不變。這時,兩流場中機翼表面對應點的壓強係數的聯繫變為:
Cp=Cp0/β
當套用於二維翼型 (或無限翼展直機翼,λ=∞,χ=0,η=1)時,後一公式給出了同一翼型在相同迎角下可壓縮與不可壓縮流場中對應點壓強係數間的關係。這是L.普朗特在1930年和H.葛勞渥在1928年得到的,又稱普朗特-葛勞渥壓縮性修正公式。
上述法則也可推廣到超音速情形,只要把亞音速繞流中作為基準的不可壓縮流場(M∞=0)換成
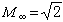 的超音速流場,而把因子β換成
的超音速流場,而把因子β換成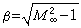 即可。
即可。 參考書目
夏皮羅著,陳立子等譯:《可壓縮流的動力學與熱力學》上冊,科學出版社,北京,1978。(A.H.Shapiro,The Dynamics and Thermodynamics of CompressibleFluid Flow,V.1,Ronald Press,New York,1953.)

