格理論的起源
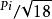 格密碼
格密碼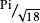 格密碼
格密碼格理論的研究源於 1611 年克卜勒提出的如下猜想: 在一個容器中堆放等半徑的小球所能達到的最大密度是. 1840 年前後 , 高斯引進了格的概念並證明 : 在三維空間堆球 , 如果所有的球心構成一個格 , 那么堆積密度所能達到的最大值是 . 在過去的一個半世紀中 , Minkowski 、 Hermite 、Bourgain 、 Hlawka 、Kabatyansky 、 Levenstein 、 Lovasz 、 Mahler 、 Rogers 等著名數學家系統地發展了一般幾何體的格堆積與覆蓋理論 . 在這一發展過程中 , 確定一個給定幾何體的最大格堆積密度和最小格覆蓋密度一直是這一學科的核心問題 .
格密碼研究現狀
第一個基於格的密碼體制是 1997 年提出的 Ajtai-Dwork 密碼體制. 該體制的安全性基於 Ajtai的 average-case 到 worst-case 的歸約 . 之後 , Goldreich, Goldwasser 和 Halevi [84] 提出了更實用的 GGH 密碼體制 . 設計者先選擇一組短的格基 , 生成格 , 然後將短的格基隨機化生成另一組格基作為公開密鑰 ,短 的 格 基 是 秘 密 密 鑰 . 但 是 這 種 方 法 生 成 的 格 不 是 Ajtai 提 出 的 那 類 隨 機 困 難 格 . 雖 然 後 來Micciancio對 GGH 的格基生成算法進行了改進 , 這個體制的安全性仍然沒有證明 .
1999 年 Ajtai 提出了一種構造隨機格和它的短格基的方法. 這種生成方案有一個很重要的優勢 ,這類隨機格服從合適的分布而且是 Ajtai 於 1996 年提出的那一類具有可證明安全性的隨機格 . 具體地說 , 給出了一種構造隨機格和它對應的垂直格的線性無關短向量組的方法。
直到 2008 年 Gentry, Peikert 和 Vaikuntanathan才開始用這種構造作為陷門設計密碼體制 .他們在論文中提出了一種基於格困難問題SIS的單向陷門函式 . 核心思想是給出了一種原像取樣的方法 . 具體地說 , 使用高斯採樣使得在擁有陷門的情況下求得原像 . 文中提出一種有效算法 , 在格基給定的情況下 , 按離散高斯分布取格點 , 標準差由格基施密特正交化的長度決定 . 這裡構造的單向陷門函式是基於SIS的 . 平均情況的SIS問題可以多項式時間歸約到最壞情況的格困難問題 SIVP. 可用於設計數字簽名 , 基於身份的加密方案等 .
2012 年 , Micciancio 等人改進了文獻 中基於格問題的單向陷門函式生成方法 . 新的生成方案更快 , 更簡潔 , 生成的單向函式困難性更高 . 該方法主要用來生成 LWE 的單向陷門函式 . 不僅如此 ,該方法在經過一些矩陣變換之後 , 可以和文獻 的方法相類似 , 生成SIS問題的單向函式和陷門 . 這裡的陷門就是對偶格的一組短格基 . 所不同的是 , 新的方案生成的短格基在經過施密特正交化之後 ,長度更短 , 因此從某種意義上來說 , 新方法生成的陷門更好 . 從參數方面具體來說 , 兩個衡量指標 , m約為 2 n log q , s 約為 1.6 n log q , 均比文獻 的方法最佳化了 . 文中最佳化了以往的高斯採樣技術 , 使得採樣過程可以並行化進行 , 時間複雜度更低 . 同時也使得 s 更小 . 主要的最佳化手段是使用了sub-Gaussian 分布的相關性質 . 之所以採用高斯採樣求得原像 , 而不是採用確定性的 nearest-plane 算法 ,是為了保證不泄露陷門的信息 .
