提出
當閉環系統沒有零點與極點相消時,閉環特徵方程式的根就是閉環傳遞函式的極點,我們常簡稱為閉環極點。因此,從已知的開環零、極點位置及某一變化的參數來求取閉環極點的分布,實際上就是解決閉環特徵方程式的求根問題。當特徵方程的階數高於四階時,除了套用MATLAB軟體包,求根過程是比較複雜的。如果要研究系統參數變化對閉環特徵方程式根的影響,就需要進行大量的反覆計算,同時還不能直觀看出影響趨勢。因此對於高階系統的求根問題來說,解析法就顯得很不方便。
1948年,W.R.伊文思在“控制系統的圖解分析”一文中,提出了根軌跡法。當開環增益或其他參數改變時,其全部數值對應的閉環極點均可在根軌跡圖上簡便地確定。因為系統的穩定性由系統閉環極點唯一確定,而系統的穩態性能和動態性能又與閉環零、極點在s平面上的位置密切相關,所以根軌跡圖不僅可以直接給出閉環系統時間回響的全部信息,而且可以指明開環零、極點應該怎樣變化才能滿足給定的閉環系統的性能指標要求。除此而外,用根軌跡法求解高階代數方程的根,比用其他近似求根法簡便。
重要性
根軌跡與系統穩定性
1.如果根軌跡全部位於s平面左側,就表示無論增益怎么改變,特徵根全部具有負實部,則系統就是穩定的。
2.如果根軌跡在虛軸上,表示臨界穩定,也就是不斷振盪。
3.如果根軌跡根軌跡全部都在s右半平面,則表示無論選擇什麼參數,系統都是不穩定的。
也就是說增益在一定範圍內變化時,系統可以保持穩定,但是當增益的變化超過這一閾值時,系統就會變得不穩定,而這一閾值就是出現在根軌跡與虛軸的交點上,在這一點系統臨界穩定。最終可由增益的取值範圍判斷系統的穩定性。
繪製法則
根軌跡的繪製具有以下繪製法則 :
法則1.起點和終點
根軌跡的起點和終點。根軌跡起於開環極點(包括無限極點),終於開環零點(包括無限零點)。
法則2.分支數、對稱性和連續性
根軌跡的分支數、對稱性和連續性。根軌跡的分支數與開環有限零點數m和有限極點數n中的大者相等,它們是連續的並且對稱於實軸。
法則3.漸近線
根軌跡的漸近線。當開環有限極點數n大於有限零點數m時,有n-m條根軌跡分支沿著與實軸交角為
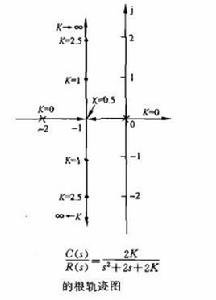
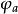 根軌跡
根軌跡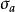 根軌跡
根軌跡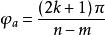 根軌跡
根軌跡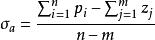 根軌跡
根軌跡、交點為 的一組漸近線趨向無窮遠處,且有 ,k=0,1,2,...,n-m-1和
法則4.在實軸上的分布
根軌跡在實軸上的分布。實軸上的某一區域,若其右邊開環實數零、極點個數之和為奇數,則該區域必是根軌跡。
法則5.分離點與分離角
根軌跡的分離點與分離角。兩條或兩條以上根軌跡分支在s平面上相遇又立即分開的點,稱為根軌跡的分離點,分離點的坐標d是下列方程的解:
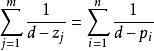 根軌跡
根軌跡式中,zj為各開環零點的數值;pi為各開環極點的數值;分離角為(2k+1)π/l
法則6.起始角與終止角
根軌跡的起始角與終止角。根軌跡離開開環複數極點處的切線與正實軸的夾角,稱為起始角;根軌跡進入開環複數零點處的切線與正實軸的夾角,稱為終止角。這些角度都可以由特定關係式求出。
法則7.與虛軸的交點
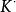 根軌跡
根軌跡根軌跡與虛軸的交點。若根軌跡與虛軸相交,則交點上的值和ω值可用勞斯判據確定,也可令閉環特徵方程中的s=jω,然後分別令其實部和虛部為零而求得。
法則8.根之和
根之和。
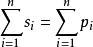 根軌跡
根軌跡