柱函式

柱函式(cylindrical function)是滿足遞推關係的一類特殊函式的總稱。

定義

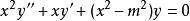柱函式

貝塞爾方程 的特解。

分類

m階貝塞爾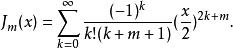函式：

柱函式

m階諾依曼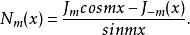函式：

柱函式

m階漢克爾函式：

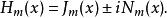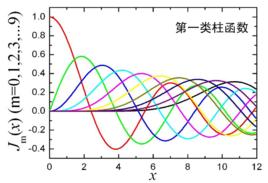
柱函式

柱函式的圖像

貝塞爾函式

貝塞爾函式圖如圖1所示：

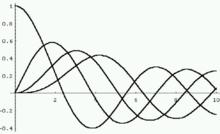圖1 貝塞爾函式

諾依曼函式

諾依曼函式圖如圖2所示：

圖2 諾依曼函式

柱函式的性質

對稱性

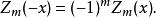柱函式

對整數階柱函式有

漸進性質

x→0時的行為：

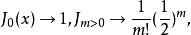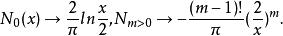柱函式

柱函式

x→∞時的行為：

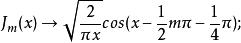柱函式

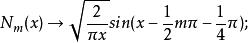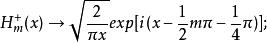柱函式

柱函式

零點分布

m階貝塞爾函式有無限多個正零點，

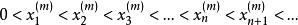柱函式

第一個正零點的大小隨著貝塞爾函式的階數增加，

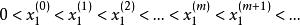柱函式

相鄰階貝塞爾函式的正零點交替出現，

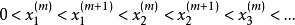柱函式

在x較大時，

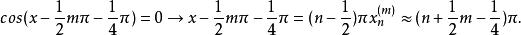柱函式

遞推公式

基本遞推公式：

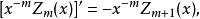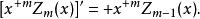柱函式

柱函式

推輪一：

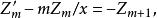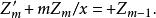柱函式

柱函式

推論二：

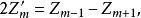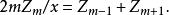柱函式

柱函式

一般柱面問題

先把非對稱的條件分解為三角函式；

含三角函式的條件求出對稱柱面解；

再對所得對稱柱面解進行疊加。

1.

先把非對稱的條件分解為三角函式；

2.

含三角函式的條件求出對稱柱面解；

3.

再對所得對稱柱面解進行疊加。