提出
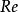柯爾莫哥洛夫理論
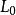柯爾莫哥洛夫理論
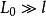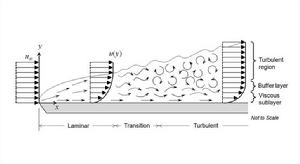
柯爾莫哥洛夫理論假如流體向各方面無限擴展，則在大 （雷諾數）值時，可以認為湍流渦旋運動的隨機特徵是各向同性的。但實際上，這種條件很少能被滿足：一方面，流動會受到固體邊界的限制；另一方面，流動的總能量也不可能無限制擴大，量級為 的大渦旋運動肯定不是各向同性的，但對於小渦旋，整體運動的影響迅速下降。當 ，且考察區域離固體邊界足夠遠時，運動就可被認為是各向同性的。在建立湍流的統計理論過程中，柯爾莫哥洛夫於1941年提出了3個基本假設。上面的討論就是他的第一假設的內容：雖然流動整體式非各向同性的，但在給定的微小區域內，可以近似的把它看作是各向同性的。
第一假設
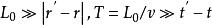柯爾莫哥洛夫理論
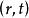柯爾莫哥洛夫理論
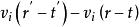柯爾莫哥洛夫理論這個假設的原始表述是：在 限定的區域內，在空間 有任意個有限點集中，差值 的機率分布保持不變。
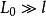柯爾莫哥洛夫理論
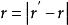柯爾莫哥洛夫理論實質上，此假設表述了整體運動的穩定態。如果此條件滿足，則湍流運動可以認為是準穩定的。準穩定態意味著，對於尺度 的渦旋，運動的隨機特徵隨時間的變化是相當緩慢的，在渦旋特徵時間內，隨機特徵可以看作是不變的。進而在主要研究物理量的空間相關時，可以暫不考慮時間因素，其統計特徵僅依賴於 。根據隨機矢量場理論，可以用橫向、縱向結構函式來作為局部各向同性湍流的基本統計量，即
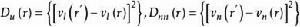柯爾莫哥洛夫理論
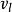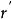柯爾莫哥洛夫理論
柯爾莫哥洛夫理論
柯爾莫哥洛夫理論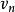
柯爾莫哥洛夫理論式中， 是速度矢量在 和 連線上的分量； 則是速度矢量在該連線垂直平面上的投影。
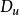柯爾莫哥洛夫理論對於氣體而言，當流速小於音速時，總可以把氣體看作是不可壓縮的，因此大氣湍流場表現為一個管矢量場，可見只需要研究 就可以了。
第二假設
柯爾莫哥洛夫理論 柯爾莫哥洛夫理論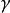
柯爾莫哥洛夫理論柯爾莫哥洛夫第二假設的內容是：在局部均勻各向同性區域中，流體運動由內摩擦力和慣性力決定。由於這一假設，渦旋體系單位體積中傳遞的能量流在數值上等於能量耗散率 ，與此相應，運動統計特徵可以依賴的參數只有 和運動粘性係數 。
第三假設
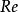柯爾莫哥洛夫理論
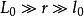柯爾莫哥洛夫理論柯爾莫哥洛夫第三假設的內容是：在大 值時，存在稱為慣性範圍的尺度區間 ，在此範圍內，內摩擦力的影響是不重要的，因而可以略去，運動圖像由慣性力決定。
