材料的強度理論
正文
材料在複雜的應力狀態下，其強度不可能都通過實驗測定，因此需要對材料發生強度破壞(失效)的力學因素作出假說，以便利用材料在簡單應力狀態（拉伸、壓縮）或少數複雜的應力狀態下的強度，推斷同一材料在各種複雜的應力狀態下的強度。這種假說和由此建立的失效準則稱為材料的強度理論或力學強度理論，後者用以強調這類理論是以巨觀的力學因素為依據，有別於從研究微觀物質構造建立的物理強度理論。材料的強度破壞分為脆性斷裂和塑性流動兩種形式。一些基本的強度理論只適用於某一形式的強度破壞。最大拉應力理論（第一強度理論） 認為在任何應力狀態下材料脆斷是由於三個主應力 σ1、σ2、σ3中最大的拉伸主應力σ1達到該材料的極限值所致；相應的強度條件則為σ1≤〔σ〕，〔σ〕為材料的容許應力。
最大伸長線應變理論（第二強度理論） 以三個主應變中最大的伸長線應變ε1達到該材料的極限值作為判別脆斷的準則；相應的強度條件為 【σ1-v(σ2+σ3)】 ≤〔σ〕，v為泊松比。這個理論雖然從形式上看似較第一強度理論完善，但與實驗結果不甚符合，如今已較少使用。
最大剪應力理論(第三強度理論) 認為材料發生塑性流動(包括剪斷)是由於最大剪應力τ
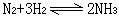＝(σ1-σ3)/2達到該材料的極限值所致；相應的強度條件為(σ1-σ3)≤〔σ〕。這個理論由於忽略中間主應力 σ2的影響所導致的誤差，對於鋼材，根據二向應力狀態下的強度試驗數據，最大為10％，且偏於安全。此理論不能套用於拉、壓流動極限不相等的材料。 形狀改變比能理論（通常稱第四強度理論） 以材料單位體積內對應於形狀改變的那部分應變能（形狀改變比能）達到極限值作為材料發生塑性流動的準則；相應的強度條件則為
莫爾強度理論 可用於拉、壓強度不相等的材料，是一個直接以材料的破壞試驗結果為依據而建立的帶一定經驗性的理論。按照此理論，首先應根據某些應力狀態下材料發生強度破壞時的最大主應力σ1和最小主應力σ3 繪出各該應力狀態下的極限應力圓(忽略中間主應力σ2)。然後作出一組極限應力圓的包絡線(圖1)。而任何應力狀態下材料發生強度破壞的準則為表示該應力狀態的應力圓(根據σ1、σ3)與極限包絡線相切。作為近似，極限包絡線可用切於單向拉伸和單向壓縮極限應力圓的直線代替，即簡化極限包絡線。這樣,上述破壞準則便可利用幾何關係（圖2）以簡單的公式表示，而相應的強度條件為
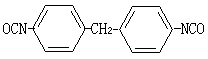，式中〔σ1〕、〔σa〕為材料在單向拉伸和壓縮時的容許拉應力和壓應力。此理論也由於忽略σ2的影響而有一定誤差。 
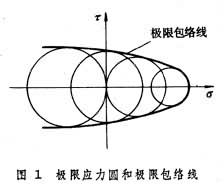材料的強度理論
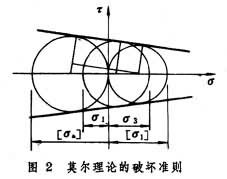材料的強度理論