概念
可微映射度(degree of differential map)是重要的同倫不變數。設(M,ω),(N,θ)均為緊緻無邊有向n維微分流形,N是連通的,f:M→N是可微映射。若p∈M是f的正則點,記:
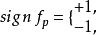 可微映射度
可微映射度則:
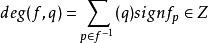 可微映射度
可微映射度其中q∈N是f的正則值。若f (q)=∅,則deg(f,q)=0.於是,deg(f,q)與正則值q∈N的選取無關,因此可記deg(f)=deg(f,q),並稱它為可微映射f的映射度,它與f(看做連續映射)的布勞威爾度一致。直觀上說,f:M→N的映射度表示f把M“覆蓋”N的次數。映射度在代數拓撲、微分拓撲中有廣泛套用,例如,證明布勞威爾不動點定理、代數基本定理等。映射度的一個主要性質是:若f光滑同倫於g:M→N,則deg(f)=deg(g).一般地,若f:M→N為連續映射,則存在與f同倫的C映射g:M→N.取q∈N是g的正則值,定義deg(f)=deg(g,q),它與g,q的選取無關。
注意,若M,N不是可定向流形,f:M→N為連續映射,則取與f同倫的C映射h:M→N,對於h的正則值q∈N,記deg(h,q)為h(q)M中點的個數的模2剩餘類,它與h,q的選取無關,於是,稱deg(f)=deg(h,q)為f的模2映射度。下述霍普夫定理表明映射度在映射的同倫分類上的本質意義。若M是緊緻連通的n維(無邊)微分流形,n≥1,f,g:M→S為連續映射,則:
1.若M是有向的,則fgdeg(f)=deg(g)。
2.若M是不可定向的,則fgdeg(f)=deg(g)。
同倫
同倫論是拓撲學的重要概念。應該指出,映射的同倫關係是從拓撲空間X到Y的所有連續映射所成集合上的一個 等價關係,它將這些映射分成一些等價類,稱每個等價類為一個同倫類。研究映射的同倫分類問題是同倫論的基本內容之一。
代數拓撲學中研究與連續映射的連續形變有關的各種課題,是代數拓撲學的一個主要組成部分。同倫概念的直觀解釋就是連續變形,以此為基礎定義的基本群被稱為同倫群。最早論及同倫群的是法國數學家龐加萊,他於1895年引進的復形基本群被稱為第一同倫群。1912年荷蘭數學家布勞威爾引入同維流形之間映射的度以研究同倫分類,開創不動點理論。20世紀20年代德國數學家霍普夫探討了球面同倫理論。20世紀30年代波蘭數學家胡雷維奇建立了群的同倫理論,引進拓撲空間的n維同倫群。另一位波蘭數學家博蘇克於1936年定義了從拓撲空間到n維球面的映射類的和,由此得到博蘇克上同倫群。20世紀40年代原蘇聯數學家龐特里亞金給出從(n+k)維球到n維球的映射同倫分類,被稱為龐特里亞金類。20世紀50年代初,法國數學家塞爾提出了研究同倫群的新方法,利用纖維化的譜序列,取得了球面同倫群計算的突破性進展。20世紀50年代末英國數學家J.F.亞當斯提出新的譜序列,成為研究同倫論的重要工具。20世紀60年代初廣義同調論的發展使同調的問題可以轉化為同倫的問題,從此代數拓撲學的這兩個主要分支統一起來,共同獲得重大發展。
布勞威爾度
布勞威爾度是對有限維空間中的連續映射建立的拓撲度。設X是有限維(實)賦范線性空間,Ω是X中的有界開集,f:Ω-→X是連續映射,p∈X\f(∂ Ω).那么可定義一個整數,記為deg(f,Ω,p),稱之為f在Ω上對點p的拓撲度.它具有下述基本性質:
1.標準性。當p∈Ω時,deg(I,Ω,p)=1,其中I為X上的恆同映射。
2.區域可加性。若Ω,Ω是Ω的不交開子集,p∈X\f(Ω-\(Ω∪Ω)),則
deg(f,Ω,p)=deg(f,Ω,p)+deg(f,Ω,p)。
3.雙同倫不變性。若h:Ω-×[0,1]→X連續及θ:[0,1]→X連續,且θ(t)∉h(∂ Ω)(ᗄt∈[0,1]),其中h(·)=h(·,t),則deg(h,Ω,θ(t))與t∈[0,1]無關。
布勞威爾度具有惟一性,即對於有限維空間中的連續映射而言,具有上述三性質的整值函式deg是惟一確定的。
性質3等價於下述兩性質4和5:
4.同倫不變性。若h:Ω-×[0,1]→X連續,且p∉h(∂ Ω)(ᗄt∈[0,1]),則deg(h,Ω,p)與t無關。
5.平移不變性。若f:Ω-→X連續,p∉f(∂Ω),令g(x)=f(x)-p,則deg(f,Ω,p)=deg(g,Ω,0)。
微分流形
設M是仿緊豪斯道夫 (Hau-sdorff)空間,且是拓撲流形,稱A= {(U,Ф)|α∈P}是它的地圖,如果{U|α∈P}是M的開覆蓋,Ф是從U到n維歐氏空間R的某開集上的同胚。(U,Φ)稱為坐標卡。如果兩個坐標卡 (U,Ф),(Uβ,Φ) 滿足U∩U≠Φ,則稱Φ·Ф:Φ(U∩U) →Φ(U∩U) 和Φ·Φ: Φβ(U∩U) →Ф(U∩U) 為U∩U上的坐標變換。如果A的所有坐標變換都是C可微的,則稱A為一個C地圖,其中1≤r≤∞。r也可等於ω,此時A稱為解析地圖。拓撲流形M的坐標卡 (U,Φ) 稱為與A是Cr相容的,如果任意(U,Φ) ∈A,坐標變換Φ·ΦΦ·Φ均C可微。拓撲流形M的C地圖A稱為最大的,如果它包含M的所有與之C相容的坐標卡。M上的最大C地圖A稱為M的C微分結構。(M,A)稱為C微分流形,或簡稱為C流形。當r=∞時,C微分結構也稱為光滑結構,C流形也稱為光滑流形。r=ω時,C結構也稱為解析結構,C流形稱為解析流形。C流形(M,A)有時也簡記為M。
從直觀上看,拓撲流形是局部歐氏空間,局部之間用同胚映射(坐標變換)貼上在一起。n維C流形,不僅局部同胚於n維歐氏空間,而且局部之間是用C光滑、且其逆也C光滑的坐標變換貼上在一起。
兩個C流形M和N,f:M→N是連續映射,且任一點P∈M,有包含P點的M中的坐標卡(U,Φ)以及包含f(P)的N中的坐標卡(V,),使得f(U)⊂V,同時,映射°f°Φ:Φ(U)→(V)是C光滑的(1≤r≤∞或r=ω),則稱f是C映射。C映射也稱為光滑映射,C映射也稱為解析映射。其中稱為f的局部表示。
C流形M和N之間的同胚f:M→N,如果f和f均是C映射,則稱f是C微分同胚。
