本性有界函式類

簡介

本性有界函式

若E為R 中的可測集，f(x)是E上的可測函式，且存在零集E⊂E，使得f(x)在E\E0上有界，則稱f(x)為E上的本性有界函式。

本性有界函式類

本性有界函式類又稱L空間，是在一個零集之外有界的函式的全體。

這樣函式的全體稱為E上的本性有界函式類，記為L (E)或L 。

範數

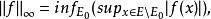本性有界函式類

對f(x)∈L (E)，定義f(x)的L 範數為其中E為E的零子集，下確界是對所有可能的這種子集E而取的：

1、若{f(x)}⊂L (E)，則{f(x)}在L (E)中收斂於f(x)等價於{f(x)}在E上除一個零集之外一致收斂於f(x)。

2、L (E)是巴拿赫空間。

3、L (E)不自反。

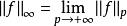本性有界函式類

4、設m(E)<+∞，若f(x)∈L (E)，則f(x)屬於一切L (E)(1≤p<+∞)，且。

5、L 空間是不可分的。