L無限空間

L無限空間(L無限 space)亦稱本性有界函式類.

簡介

在一個零集之外有界的函式的全體.若E為R”中的可測集，f<x)是E上的可測函式，且存在零集ESCE，使得f(二)在E\E。上有界，則f(二)稱為E上的本性有界函式.這樣函式的全體稱為E上的I.，空間，記為

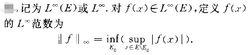L無限空間

其中E。為E的零子集，下確界是對所有可能的這

種子集E。而取的:

1.若{人(二)}CL0" (E)，則{人(二)}在L0' ( E)中

收斂於f (x)等價於{f.,(二)}在E上除一個零集之

外一致收斂於f<x).

2. L0} (E)是巴拿赫空間.

3. L}0 (E)不自反.

4.設m(E)<+二，若f<x)EL`}'<E)，則f<x)

屬於一切

L無限空間

5. L一空間是不可分的，關於“可分”詳見本卷

《泛函分析》同名條.