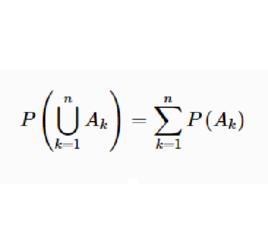定義
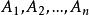 有限可加性
有限可加性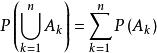 有限可加性
有限可加性若是兩兩互不相容的事件,則有,即有限個兩兩互不相容事件的和事件的機率,等於每個事件機率的和。
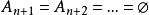 有限可加性
有限可加性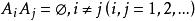 有限可加性
有限可加性證明: 令,則有,根據機率的可列可加性和性質1得
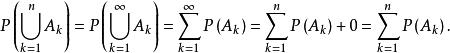 有限可加性
有限可加性相關性質定理
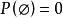 有限可加性
有限可加性性質1:。
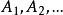 有限可加性
有限可加性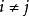 有限可加性
有限可加性 有限可加性
有限可加性性質2:(可列可加性)設是兩兩互不相容的事件,即當時,,則有
 有限可加性
有限可加性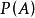 有限可加性
有限可加性 有限可加性
有限可加性那么稱為事件的機率。
套用舉例
證明對立事件機率的公式
 有限可加性
有限可加性(對立事件的機率)對於任意一個事件A,有.
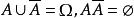 有限可加性
有限可加性證明: 由於,根據機率的 有限可加性,得
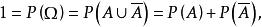 有限可加性
有限可加性 有限可加性
有限可加性所以。
證明機率加法公式
對於任意兩事件A,B,有
 有限可加性
有限可加性這個式子通常稱為 機率加法公式。
證明思路:利用有限可加性的前提是兩個求和的事件互不相容,為此,應把任意兩個事件A與B的和表示成兩個互不相容的事件的和,然後利用有限可加性即得,這種方法是十分典型的,可稱之為“拆分法”。
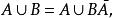 有限可加性
有限可加性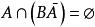 有限可加性
有限可加性證明: 因為,其中,所以
 有限可加性
有限可加性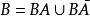 有限可加性
有限可加性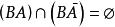 有限可加性
有限可加性但是,,且,有
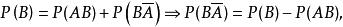 有限可加性
有限可加性故結論得證。
證明減法公式
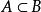 有限可加性
有限可加性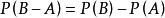 有限可加性
有限可加性(減法公式)(1) 設A,B是兩個事件,若,則有;
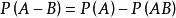 有限可加性
有限可加性(2) 對於任意兩個事件A,B,有。
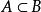 有限可加性
有限可加性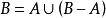 有限可加性
有限可加性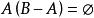 有限可加性
有限可加性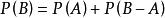 有限可加性
有限可加性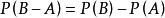 有限可加性
有限可加性證明:(1)由知道,,且,根據機率的有限可加性。得,所以。
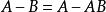 有限可加性
有限可加性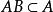 有限可加性
有限可加性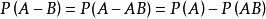 有限可加性
有限可加性(2)由於,且,根據(1)則有。