定義
(1)有效值即瞬時值的平方的平均值的平方根,也簡稱為方均根值。
(2) 對於電流(或電壓)也可以按下述定義,與(1)中的定義等效:讓一個交流電流(電壓)和一個直流電流(電壓)分別加到阻值相同的電阻上,如果在相同周期內產生的熱量相等,那么就把這一直流電流(電壓)的數值叫做這一交流電流(電壓)的有效值。
可以證明有以下結論:
正弦量的有效值等於其最大值被2的平方根去除。
非正弦量的有效值,等於它的直流分量、基波和各高次諧波有效值平方和的平方根值(還有一種定義方式,將直流分量、基波定義分別為零次諧波和一次諧波。在這個前提下,非正弦量的有效值就等於它的各次諧波有效值平方和的平方根值)。
電流熱效應
有效值是根據電流熱效應來規定的,讓一個交流電流和一個直流電流分別通過阻值相同的電阻,如果在相同時間內產生的熱量相等,那么就把這一直流電的數值叫做這一交流電的有效值。
在電工技術中,有時並不需要知道交流電的瞬時值,而規定一個能夠表征其大小的特定值——有效值,其依據是交流電流和直流電流通過電阻時,電阻都要消耗電能(熱效應)。
常見測量方法
峰值檢測法
用峰值檢測電路測量信號峰值,再除以波峰因數(1.414),得到信號有效值。
特點:僅適合正弦波。
整流平均法
對測量信號進行全波整流,然後用積分電路求得信號的平均值,再乘以波形因數(1.1107),得到信號有效值。
特點:僅適合正弦波。
真有效值法
直接測量信號的方均根值。
特點:適應任意波形。
FFT變換法
先對信號進行高速採樣,然後用FFT對其進行分析,得出直流分量、基波和各次諧波的有效值,再求它們平方和的平方根,最後得出信號的有效值。
特點:適合任意波形。不但可得出信號的有效值,還可以得出直流分量,基波和各次諧波的有效值。
1.峰值檢測法
用峰值檢測電路測量信號峰值,再除以波峰因數(1.414),得到信號有效值。
特點:僅適合正弦波。
2.整流平均法
對測量信號進行全波整流,然後用積分電路求得信號的平均值,再乘以波形因數(1.1107),得到信號有效值。
特點:僅適合正弦波。
3.真有效值法
直接測量信號的方均根值。
特點:適應任意波形。
4.FFT變換法
先對信號進行高速採樣,然後用FFT對其進行分析,得出直流分量、基波和各次諧波的有效值,再求它們平方和的平方根,最後得出信號的有效值。
特點:適合任意波形。不但可得出信號的有效值,還可以得出直流分量,基波和各次諧波的有效值。
套用實例
設正弦交流電流 i( t)在一個周期 T時間內,使一電阻 R消耗的電能為 QR,另有一相應的直流電流 I在時間 T內也使該電阻 R消耗相同的電能,即 QR = I2RT。就平均對電阻作功的能力來說,這兩個電流( i與 I)是等效的,則該直流電流 I的數值可以表示交流電流 i( t)的大小,於是把這一特定的數值 I稱為交流電流的有效值。理論與實驗均可證明,正弦交流電流 的有效值 I等於其振幅(最大值) Im的0.707倍。
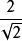 有效值
有效值例如正弦交流電流 i = 2sin( wt - 30°) A的有效值I ==2×0.707 = 1.414 A,如果交流電流 i通過R = 10 歐姆 的電阻時,在一秒時間內電阻消耗的電能(又叫做平均功率)為P = I²R= 20 W,即與I = 1.414 A的直流電流通過該電阻時產生相同的電功率。
因為正弦交流電的有效值與最大值(振幅值)之間有確定的比例係數,所以幅值、頻率、初相這三個參數也可以合在一起叫做正弦交流電的三要素。