周期信號分析
一個周期信號可以通過傅立葉變換分解為直流分量c0和不同頻率的正弦信號的線性疊加：
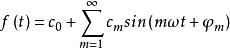基波有效值其中，cm表示m次諧波的幅值，其角頻率為mω，初始相位為φm，其有效值為cm/√2。
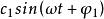基波有效值當m=1時，為基波分量的表達式，其角頻率為ω，初始相位為φ1，其方均根值c1/√2稱為基波有效值。
ω/2π為基波分量的頻率，稱為基波頻率，基波分量的頻率等於交流信號的頻率。而m次諧波的頻率為基波頻率的整數倍（m倍）。
測量方法
測量設備當信號的諧波頻率與基波頻率差距較大時，即信號的低次諧波含量較小，主要為高次諧波時，可以通過低通濾波的方法將高次諧波濾除，剩下就是信號的基波，採用均值檢波表、峰值檢波表和真有效值檢波表均可測量其有效值，測量結果近似等於基波有效值。
當信號頻譜較複雜時，尤其是低次諧波含量較大時，很難用濾波的方法將基波準確分離，一般先用交流採樣獲取離散時間信號序列，再用離散傅立葉變換（DFT或FFT）對其進行傅立葉展開，即可求得基波有效值。各種諧波分析儀和寬頻功率分析儀（變頻功率分析儀、高精度功率分析儀等）等設備均可測量適用頻率範圍內交流信號的基波有效值。上述儀器除了測量電壓、電流的基波有效值之外，還具備功率測量及諧波測量功能。
