定義
線性方程組
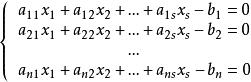 最小二乘解
最小二乘解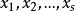 最小二乘解
最小二乘解可能無解。即任意一組 都可能使
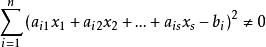 最小二乘解
最小二乘解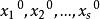 最小二乘解
最小二乘解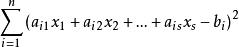 最小二乘解
最小二乘解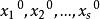 最小二乘解
最小二乘解我們設法找到 使 最小,這樣的 稱為方程組的最小二乘解。這種問題叫做最小二乘問題。
代數條件
下面利用歐式空間的概念來表達最小二乘法,並給出最小二乘解所滿足的代數條件。
 最小二乘解
最小二乘解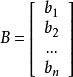 最小二乘解
最小二乘解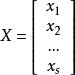 最小二乘解
最小二乘解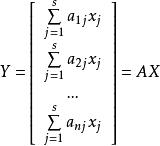 最小二乘解
最小二乘解令 , , ,
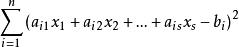 最小二乘解
最小二乘解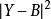 最小二乘解
最小二乘解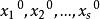 最小二乘解
最小二乘解用距離的概念, 就是 ,最小二乘法就是找到 使Y和B的距離最短。
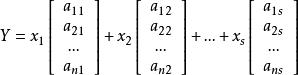 最小二乘解
最小二乘解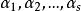 最小二乘解
最小二乘解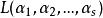 最小二乘解
最小二乘解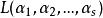 最小二乘解
最小二乘解把A的各列向量分別記為 ,由它們生成的子空間為 ,Y就是 中的向量。於是最小二乘法可以敘述為:
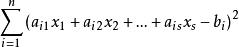 最小二乘解
最小二乘解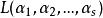 最小二乘解
最小二乘解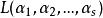 最小二乘解
最小二乘解找到X使得 就是在 中找到一向量Y,使得B到它的距離比到子空間 中其它向量的距離都短。
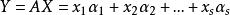 最小二乘解
最小二乘解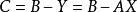 最小二乘解
最小二乘解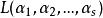 最小二乘解
最小二乘解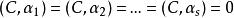 最小二乘解
最小二乘解設 使所要求的向量,則 必須垂直於子空間 。為此,只須且必須 ,由矩陣乘法,上述可寫成矩陣相乘的式子,即:
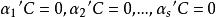 最小二乘解
最小二乘解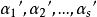 最小二乘解
最小二乘解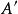 最小二乘解
最小二乘解而 按行正好排列稱矩陣 。上述一串等式合起來便是:
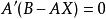 最小二乘解
最小二乘解或
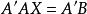 最小二乘解
最小二乘解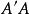 最小二乘解
最小二乘解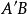 最小二乘解
最小二乘解這就是最小二乘解所滿足的代數方程,它是一個線性方程,係數矩陣是 ,常數項是 ,這種線性方程總是有解的。
示例
已知某種材料在生產過程中的廢品率y與某種化學成分x有關。下表中記載了某工廠生產中y與相應x的幾次數值:
| x(%) | 1.00 | 0.9 | 0.9 | 0.81 | 0.60 | 0.56 | 0.35 |
| y(%) | 3.6 | 3.7 | 3.8 | 3.9 | 4.0 | 4.1 | 4.2 |
要求:找出y與x的一個近似公式。
解:若把表中數值畫成圖來看,可以發現,它的變化趨勢近於一條直線,因此,我們決定選取x的一次式ax+b來表達。當然最好能選到適合的a,b,使得下面的等式:
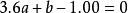 最小二乘解
最小二乘解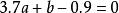 最小二乘解
最小二乘解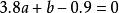 最小二乘解
最小二乘解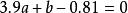 最小二乘解
最小二乘解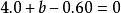 最小二乘解
最小二乘解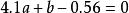 最小二乘解
最小二乘解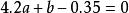 最小二乘解
最小二乘解都成立。實際上是不可能的。任何a,b代入上述各式都會發生誤差。於是想找a,b使得上面各式的誤差的平方和最小,即尋找a,b,使
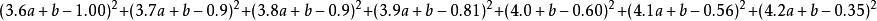 最小二乘解
最小二乘解最小。這裡的討論是誤差的平方即二乘方,故稱為最小二乘法。
將上述數值用矩陣來表示,即為:
 最小二乘解
最小二乘解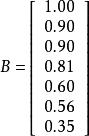 最小二乘解
最小二乘解,
最小二乘解a,b所滿足的方程是:
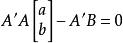 最小二乘解
最小二乘解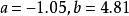 最小二乘解
最小二乘解解得: (取三位有效數字)
