定義
 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式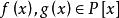 最大公因式
最大公因式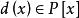 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式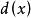 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式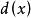 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式設 、 是數域 上的多項式,即 ,若存在 是 、 的公因式,且 是 和 所有公因式的倍式,則稱 為 和 的最大公因式,記為
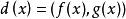 最大公因式
最大公因式所以,最大公因式有兩個含義:第一,首先是公因式;第二,又是所有公因式的倍式,即體現“最大性”。
性質
 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式①設、是數域上的多項式且不全為0,則其最大公因式一定存在。
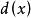 最大公因式
最大公因式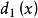 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式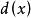 最大公因式
最大公因式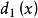 最大公因式
最大公因式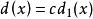 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式②若與都是和的最大公因式,那么與最多相差一個非零常數因子,即。另一方面,和的最大公因式與任意非零常數的乘積也是其最大公因式。因此,最大公因式不是唯一的,但首項係數為1的最大公因式是唯一的。
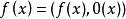 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式③,即任意的和0的最大公因式是自身。
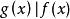 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式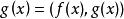 最大公因式
最大公因式④若整除,即整除,則。
輾轉相除法
輾轉相除法是求最大公因式的一種行之有效的方法,過程敘述如下:
 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式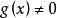 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式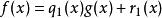 最大公因式
最大公因式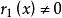 最大公因式
最大公因式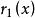 最大公因式
最大公因式 最大公因式
最大公因式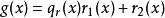 最大公因式
最大公因式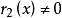 最大公因式
最大公因式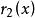 最大公因式
最大公因式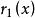 最大公因式
最大公因式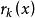 最大公因式
最大公因式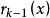 最大公因式
最大公因式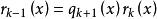 最大公因式
最大公因式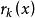 最大公因式
最大公因式 最大公因式
最大公因式 最大公因式
最大公因式設、是數域上的多項式且不全為0,不妨設。利用帶餘除法,以除得。若,再以除得。若,則又用除。如此繼續下去,每一步都至少使得餘式降低一次,經過有限次帶餘除法後,必然得到這樣一個,它整除,即。此時即為、的最大公約數。

