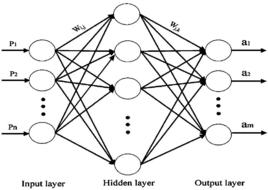
簡介
算法逼近是指利用有關算法逼近一些實際問題的場景或精確度。算法逼近在實際套用可以減少有關產品研發的成本,因為通過算法逼近可以模擬一些實驗場景或計算出一些有關問題的精確度。例如,在實際套用中,有很多問題屬於數值計算類問題,一般都是通過利用有關算法來實現數值逼近,從而解決問題。不同的問題,算法逼近使用逼近算法一般不同。
數值逼近
數值逼近是研究函式的離散逼近,用適合於計算機上的計算的簡單函式(如多項式,連分式等)逼近複雜函式。主要包括插值法、最佳一致逼近、最佳平方逼近與最小二乘逼近。各種代數插值是連續系統離散化的基礎,理論與實踐表明,分段低次插值比高次插值具有更好的穩定性。由於樣條函式具有良好的特性,已成為函式逼近的重要工具而且被廣泛套用,樣條逼近是函式逼近的一個重要研究方向。數值逼近也是初等函式子程式的重要方法 。
算法的基本特徵
一個算法應該具有以下五個重要的特徵:
有窮性(Finiteness)
算法的有窮性是指算法必須能在執行有限個步驟之後終止;
確切性(Definiteness)
算法的每一步驟必須有確切的定義;
輸入項(Input)
一個算法有0個或多個輸入,以刻畫運算對象的初始情況,所謂0個輸入是指算法本身定出了初始條件;
輸出項(Output)
一個算法有一個或多個輸出,以反映對輸入數據加工後的結果。沒有輸出的算法是毫無意義的;
可行性(Effectiveness)
算法中執行的任何計算步驟都是可以被分解為基本的可執行的操作步,即每個計算步都可以在有限時間內完成(也稱之為有效性)。
算法逼近算法
隨機逼近
隨機逼近,是在有隨機誤差干擾的情況下,用逐步逼近的方式估計某一特定值的數理統計方法。1951年,H.羅賓斯和S.門羅首先研究了此問題的一種形式:設因素 x的值可由試驗者控制, x的“回響”的指標值為 Y,當取 x之值 x進行試驗時,回響 Y可表為 Y= h( x)+ε,式中 h( x)為一未知函式,ε為隨機誤差。設目標值為 A,要找這樣的 x,使 h( x)= A。分別以 Y- A和 h( x)- A代替 Y和 h( x)。不妨設 A=0,問題就在於找方程 h( x)=0的根 x。例如若 x為施藥量, Y為衡量藥物反應的某種生理指標,則問題在於找出施藥量 x,以使該生理指標控制於適當的值 A。
樣條函式
在數學學科數值分析中,樣條是一種特殊的函式,由多項式分段定義。樣條的英語單詞spline來源於可變形的樣條工具,那是一種在造船和工程製圖時用來畫出光滑形狀的工具。在插值問題中,樣條插值通常比多項式插值好用。用低階的樣條插值能產生和高階的多項式插值類似的效果,並且可以避免被稱為龍格現象的數值不穩定的出現。並且低階的樣條插值還具有“保凸”的重要性質。在計算機科學的計算機輔助設計和計算機圖形學中,樣條通常是指分段定義的多項式參數曲線。由於樣條構造簡單,使用方便,擬合準確,並能近似曲線擬合和互動式曲線設計中複雜的形狀,樣條是這些領域中曲線的常用表示方法。
稀疏逼近
稀疏逼近是圖像處理中最基本、最核心的內容,它是圖像壓縮、圖像增強、圖像特徵提取、圖像內容檢索等圖像處理技術的基礎。稀疏逼近最簡單的定義是儘可能用最少的係數去重建逼近原始圖像 。