定義
 反么正算符
反么正算符反么正算符是反線性的么正算符的簡稱。反線性算符的定義為 滿足:
 反么正算符
反么正算符 反么正算符
反么正算符 反么正算符
反么正算符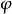 反么正算符
反么正算符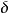 反么正算符
反么正算符這裡 、 為任一復常數, 、 為任意波函式,就是說,如將某一函式抽出算符作用之外,需要對它取複數共軛。這是與線性算符本質的差別。
性質
 反么正算符
反么正算符 反么正算符
反么正算符反線性算符 的Hermite共軛算符 的定義是:
 反么正算符
反么正算符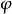 反么正算符
反么正算符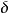 反么正算符
反么正算符這裡,為了使定義在邏輯上自洽,中間這個標積必須要有複數共軛。可作如下檢查即知這一點是必須的:構想從標積的 或 中抽出一個附屬常係數。
 反么正算符
反么正算符反線性的么正算符 (反么正算符)定義為:
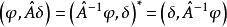 反么正算符
反么正算符根據這個定義,立即知道,對反么正算符也有
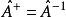 反么正算符
反么正算符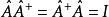 反么正算符
反么正算符這導致 。這與么正算符相同。
在時間反演變換的套用
設時間反演變換在體系態失Hilbert空間中的表示為算符T。按照經典類比,可得量子力學T算符對基本力學量組的變換
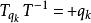 反么正算符
反么正算符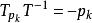 反么正算符
反么正算符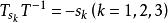 反么正算符
反么正算符按基本力學量組的含義,這組對易關係已能完全決定時間反演算符T(不計常數因子)。於是,可將它們看成是量子力學時間反演算符的定義式。
另一方面,依據Wigner定理,算符T對系統的變換不是么正的便是反么正的。若是前者則為線性算符,如為後者則是反線性算符。然而,對這兩種情況都有
 反么正算符
反么正算符首先,T算符是個反線性算符。
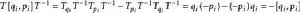 反么正算符
反么正算符證明:
 反么正算符
反么正算符於是就有 。這就是說,T必須是個反線性算符,
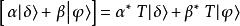 反么正算符
反么正算符反么正算符正是這種反線性的么正的算符的簡稱。
