點式收斂拓撲
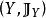 映射空間
映射空間設X為一個集合, 為一個拓撲空間.從 X到Y的所有映射構成的集合記作
 映射空間
映射空間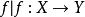 映射空間
映射空間={ 為映射}.
 映射空間
映射空間 映射空間
映射空間 映射空間
映射空間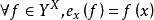 映射空間
映射空間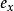 映射空間
映射空間 映射空間
映射空間實際上,它就是以X為指標集的笛卡兒積 對 ,令 為 的第x個投射,則對 恰為映射f在點x處的像,因此,我們將投射 改稱為 在點x∈X處的 賦值映射。
 映射空間
映射空間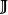 映射空間
映射空間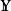 映射空間
映射空間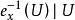 映射空間
映射空間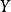 映射空間
映射空間 映射空間
映射空間 映射空間
映射空間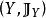 映射空間
映射空間另一方面, 的積拓撲 便是以 ={ 為 中的開集,x∈X }為子基的拓撲,並稱 為 的 點式收斂拓撲,而 稱為從集合X到拓撲空間 的 映射空間( 點式收斂拓撲)。
由於映射空間(點式收斂拓撲)是一類特殊的拓撲積空間,因此,關於拓撲積空間的一般理論全部適用於它,無須另行證明。
 映射空間
映射空間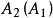 映射空間
映射空間 映射空間
映射空間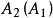 映射空間
映射空間定理1 設X為一個集合, 為一個拓撲空間,則映射空間 (點式收斂拓撲)為 空間 Y為平庸拓撲空間,或者X為至多可數集並且Y為 空間。
 映射空間
映射空間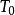 映射空間
映射空間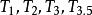 映射空間
映射空間 映射空間
映射空間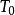 映射空間
映射空間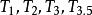 映射空間
映射空間定理2 設X為任一集合,Y為一個拓撲空間,則映射空間 (點式收斂拓撲)為 ( 正則,完全正則,連通,路連通,緊緻)空間 Y為 ( ,正則,完全正則,連通,道路連通,緊緻)空間。
對於 連續映射,我們引進
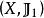 映射空間
映射空間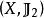 映射空間
映射空間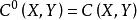 映射空間
映射空間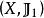 映射空間
映射空間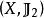 映射空間
映射空間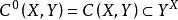 映射空間
映射空間 映射空間
映射空間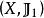 映射空間
映射空間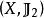 映射空間
映射空間定義2 設 與 為兩個拓撲空間, 為從 到 的所有連續映射構成的集合,則 ,C(X,Y) 作為映射空間 (點式收斂拓撲)的子拓撲空間稱為從拓撲空間 到拓撲空間 的 連續映射空間(點式收斂拓撲),並且C(X,Y) 的拓撲也稱為 點式收斂拓撲。
 映射空間
映射空間 映射空間
映射空間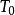 映射空間
映射空間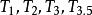 映射空間
映射空間 映射空間
映射空間 映射空間
映射空間 映射空間
映射空間 映射空間
映射空間 映射空間
映射空間C(X,Y) 作為 的子拓撲空間,自然可以繼承 的許多拓撲性質.例如,當Y為 ( ,正則、完全正則、連通、道路連通、緊緻)時,由可積性知,映射空間 (點式收斂拓撲)為 ( ,正則,完全正則、連通、道路連通、緊緻)空間,再根據遺傳性,連續映射空間C(X,Y) (點式收斂拓撲)也為 ( ,正則,完全正則、連通、道路連通、緊緻)空間。
一致收斂度量
 映射空間
映射空間定義3 設X為一個集合,﹙Y,ρ﹚ 為一個度量空間,記 為從X到Y的所有映射構成的集合,定義
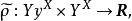 映射空間
映射空間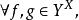 映射空間
映射空間對
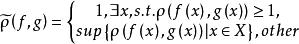 映射空間
映射空間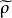 映射空間
映射空間 映射空間
映射空間 映射空間
映射空間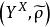 映射空間
映射空間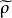 映射空間
映射空間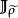 映射空間
映射空間 映射空間
映射空間容易驗證 為 的一個度量,稱它為 的 一致收斂度量,度量空間 稱為 映射空間( 一致收斂度量),由一致收斂度量 誘導出來的拓撲 稱為 的 一致收斂拓撲.拓撲空間 稱為 映射空間( 一致收斂拓撲)。
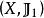 映射空間
映射空間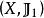 映射空間
映射空間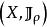 映射空間
映射空間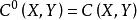 映射空間
映射空間當 為一個拓撲空間時,從 到 的所有連續映射構成的集合 作為度量空間 的子度量空間,稱為 連續映射 空間(一致收斂度量),此時它的度量也稱為 一致收斂度量;它作為拓撲空間 的子拓撲空間稱為 連續映射空間( 一致收斂拓撲),此時它的拓撲也稱為 一致收斂拓撲。
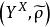 映射空間
映射空間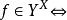 映射空間
映射空間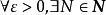 映射空間
映射空間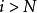 映射空間
映射空間定理3設X為集合,﹙Y,ρ﹚ 為一個度量空間.在度量空間 (一致收斂度量)中的一個序列 收斂於 序列 一致收斂於 ,即 ,當 時,
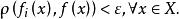 映射空間
映射空間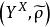 映射空間
映射空間定理4 設X為一個集合,﹙Y,ρ﹚ 為一個完備度量空間,映射空間(一致收斂度量) 也為一個完備度量空間。
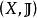 映射空間
映射空間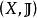 映射空間
映射空間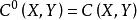 映射空間
映射空間定理5 設 為一個拓撲空間, ﹙Y,ρ﹚為一個度量空間,則從 到 的所有連續映射構成的集合 為映射空間(一致收斂拓撲)中的一個閉集,因此,度量空間C(X,Y) (一致收斂度量)也是一個完備度量空間。
緊緻-開拓撲
 映射空間
映射空間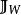 映射空間
映射空間 映射空間
映射空間 映射空間
映射空間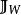 映射空間
映射空間定義4 設X與Y為兩個拓撲空間,W為X的全體緊緻子集構成的集族,則從X到Y的全體映射構成的集合 的W一開拓撲 稱為 的 緊緻一開拓撲,拓撲空間( , )稱為 映射空間(緊緻一開拓撲)。
 映射空間
映射空間 映射空間
映射空間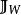 映射空間
映射空間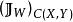 映射空間
映射空間從X到Y的全體連續映射構成的集合C(X,Y) 作為映射空間 (緊緻一開拓撲)的子拓撲空間稱為 連續映射空間(緊緻一開拓撲);並且 的緊緻一開拓撲 在C(X,Y)上的限制 也稱為C(X,Y) 的 緊緻一開拓撲。
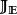 映射空間
映射空間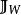 映射空間
映射空間 映射空間
映射空間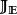 映射空間
映射空間 映射空間
映射空間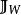 映射空間
映射空間定理6 設X與Y為兩個拓撲空間, 與 分別為從X到Y的全體映射構成的集合 的點式收斂拓撲與緊緻一開拓撲,則。
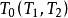 映射空間
映射空間 映射空間
映射空間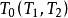 映射空間
映射空間定理7 設X與Y為兩個拓撲空間,如果Y為 空間,則映射空間 (緊緻一開拓撲)以及連續映射空間C(X,Y) (緊緻一開拓撲)也為 空間。
定理8 設X為緊緻空間,﹙Y,ρ﹚ 為一個度量空間,則連續映射空間C(X,Y) 的一致收斂拓撲與緊緻一開拓撲相同。

